Ngân hàng bài tập
SS
Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ.
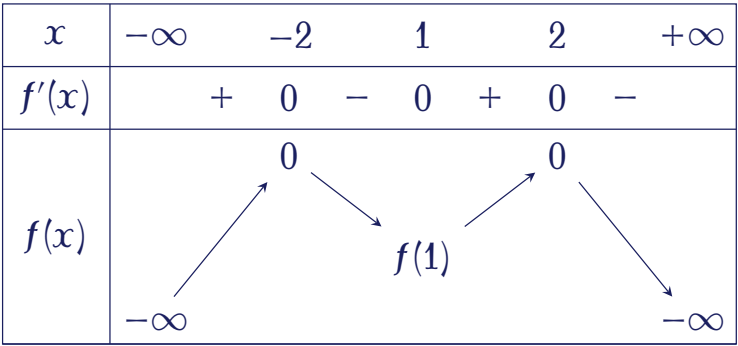
Hàm số $g(x)=\big[f(3-x)\big]^2$ nghịch biến trên khoảng nào trong các khoảng sau?
| $(-2;5)$ | |
| $(1;2)$ | |
| $(2;5)$ | |
| $(5;+\infty)$ |
1 lời giải
Chọn phương án C.
Đặt $u=3-x\Rightarrow x=3-u$.
Ta có $g'(x)=-2f'(3-x)\cdot f(3-x)=-2f'(u)\cdot f(u)$.
Cho $g'(x)<0\Leftrightarrow-2f'(u)\cdot f(u)<0\Leftrightarrow f'(u)\cdot f(u)>0$.

Dựa vào bảng xét dấu ta thấy $g(x)$ nghịch biến trên khoảng $(-\infty;1)$ và $(2;5)$.
