Ngân hàng bài tập
S
Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}$ và có đồ thị $f'(x)$ như hình vẽ.
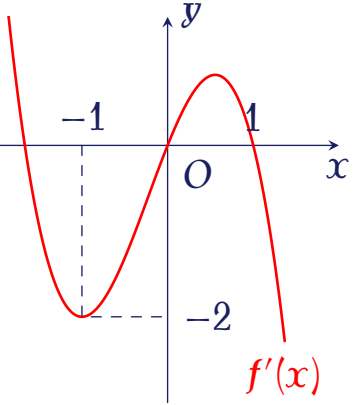
Số điểm cực trị của hàm số $y=f(x)+2x$ là
| $1$ | |
| $2$ | |
| $3$ | |
| $4$ |
1 lời giải
Chọn phương án A.
Ta có $g'(x)=f'(x)+2$.
Cho $g'(x)=0\Leftrightarrow f'(x)=-2$.
Số điểm cực trị của hàm số $g(x)$ bằng với số nghiệm bội lẻ của phương trình $g'(x)=0$.

Ta thấy đường thẳng $y=-2$ cắt đồ thị hàm số $y=f'(x)$ tại một điểm $x_0>1$ (nghiệm đơn) và tiếp xúc với đồ thị hàm số $y=f'(x)$ tại điểm $x=-1$ (nghiệm kép).
Vậy $g(x)$ có một điểm cực trị.
