Ngân hàng bài tập
SS
Cho hàm số $f(x)$, bảng biến thiên của hàm số $f'(x)$ như sau:
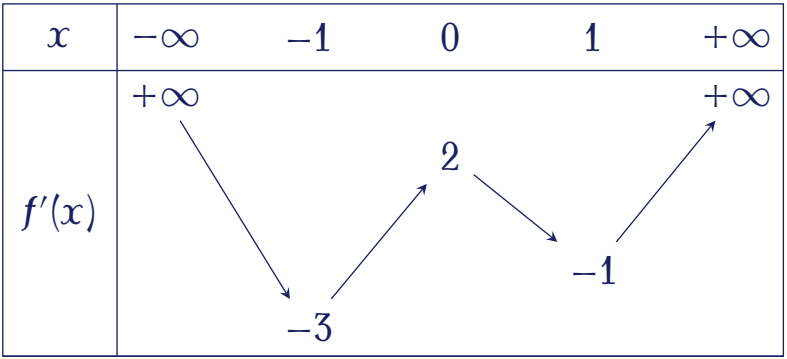
Số điểm cực trị của hàm số $f\big(x^2-2x\big)$ là
| $9$ | |
| $3$ | |
| $7$ | |
| $5$ |
1 lời giải
Chọn phương án C.
Từ bảng biến thiên ta có $$f'(x)=0\Leftrightarrow\left[\begin{array}{ll}x=a &\in(-\infty;-1)\\ x=b &\in(-1;0)\\ x=c &\in(0;1)\\ x=d &\in(1;+\infty)\end{array}\right.$$

Ta có $y'=2(x-1)f'\big(x^2-2x\big)$.
Cho $y'=0\Leftrightarrow\Leftrightarrow\left[\begin{array}{l}x-1=0\\ f'\big(x^2-2x\big)=0\end{array}\right.\Leftrightarrow\left[\begin{array}{ll}x=1\\ x^2-2x=a &(1)\\ x^2-2x=b &(2)\\ x^2-2x=c &(3)\\ x^2-2x=d &(4)\end{array}\right.$

Quan sát đồ thị hàm số $h(x)=x^2-2x$ ta thấy
- Phương trình $(1)$ vô nghiệm.
- Các phương trình $(2),\,(3),\,(4)$ đều có $2$ nghiệm, các nghiệm này phân biệt nhau.
Vậy phương trình $y'=0$ có $7$ nghiệm phân biệt, tức là hàm số $y=f\big(x^2-2x\big)$ có $7$ điểm cực trị.
