Ngân hàng bài tập
SS
Cho hàm số $y=f(x)$. Đồ thị của hàm số $y=f'(x)$ như hình vẽ.
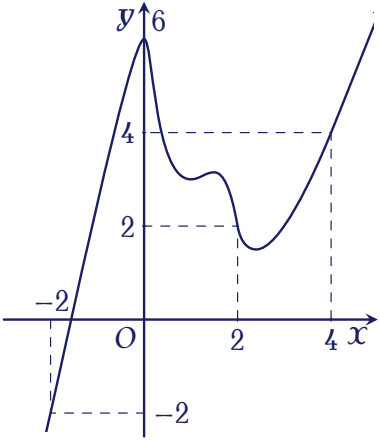
Đặt $h(x)=f(x)-x$. Mệnh đề nào dưới đây đúng?
| $\min\limits_{[-2;2]}h(x)=h(-2)$ | |
| $\max\limits_{[0;4]}h(x)=h(0)$ | |
| $\min\limits_{[-1;2]}h(x)=h(-1)$ | |
| $h(2)< h(4)< h(0)$ |
1 lời giải
Chọn phương án C.
Ta có $h'(x)=f'(x)-1$.
Cho $h'(x)=0\Leftrightarrow f'(x)=1\Leftrightarrow x=a\in(-2;-1)$.
- $h'(x)>0\Leftrightarrow f'(x)>1\Rightarrow x>a$.
- $h'(x)<0\Leftrightarrow f'(x)<1\Rightarrow x<a$.
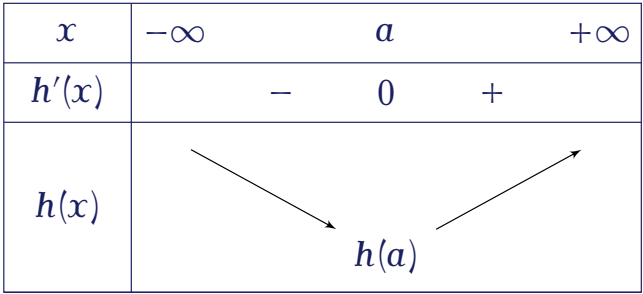
Dựa vào bảng biến thiên ta thấy $h(x)$ đồng biến trên $[-1;2]$, do đó $\min\limits_{[-1;2]}h(x)=h(-1)$.
