Ngân hàng bài tập
SS
Cho hàm số $f(x)$ có đồ thị $f'(x)$ như hình vẽ.
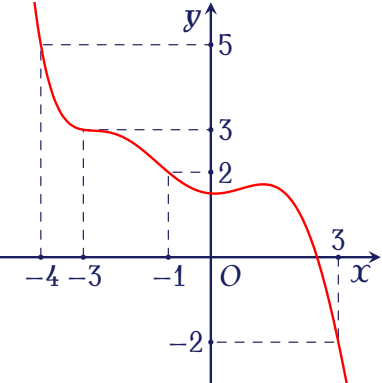
Trên đoạn $[-4;3]$, hàm số $g(x)=2f(x)+(1-x)^2$ đạt giá trị nhỏ nhất tại điểm
| $x_0=-4$ | |
| $x_0=-1$ | |
| $x_0=3$ | |
| $x_0=-3$ |
1 lời giải
Chọn phương án B.
Ta có $g'(x)=2f'(x)+2(x-1)=2\big[f'(x)-(1-x)\big]$.
Cho $g'(x)=0\Leftrightarrow f'(x)=1-x \Leftrightarrow\left[\begin{array}{ll}x=-4 &\in[-4;3]\\ x=-1 &\in[-4;3]\\ x=3 &\in[-4;3]\end{array}\right.$

- $g'(x)>0\Leftrightarrow f'(x)>1-x\Rightarrow x\in(-1;3)$.
- $g'(x)<0\Leftrightarrow f'(x)<1-x\Rightarrow x\in(-4;-1)$.
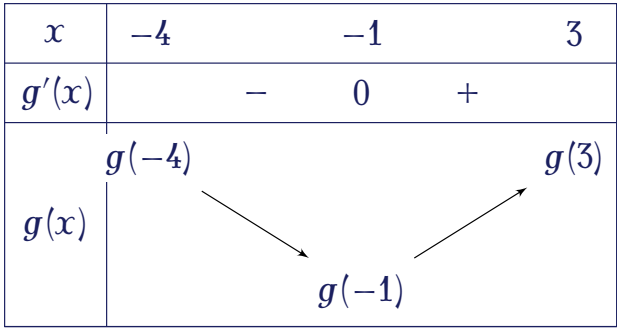
Vậy $g(x)$ đạt giá trị nhỏ nhất trên đoạn $[-1;3]$ tại điểm $x=-1$.
