Cho hàm số $y=f(x)$ có đạo hàm $y=f'(x)$ với đồ thị như hình vẽ.
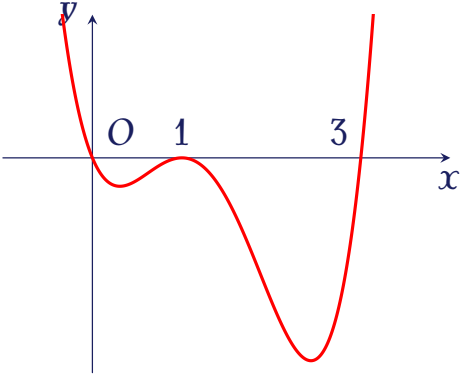
Tìm $m$ để hàm số $g(x)=f\big(x^2+m\big)$ có $3$ điểm cực trị.
| $m\in(-\infty;0]$ | |
| $m\in(3;+\infty)$ | |
| $m\in[0;3)$ | |
| $m\in(0;3)$ |
Chọn phương án D.
Ta có $f'(x)=0\Leftrightarrow\left[\begin{array}{ll}x=0\\ x=1 &\text{(nghiệm kép)}\\ x=3\end{array}\right.$
Lại có $g'(x)=2xf'\big(x^2+m\big)$.
Cho $\begin{aligned}[t]
g'(x)=0&\Leftrightarrow\left[\begin{array}{l}2x=0\\ f'\big(x^2+m\big)=0\end{array}\right.\\
&\Leftrightarrow\left[\begin{array}{l}x=0\\ x^2+m=0\\ x^2+m=3\end{array}\right.\\
&\Leftrightarrow\left[\begin{array}{l}x=0\\ m=-x^2\\ m=-x^2+3\end{array}\right.
\end{aligned}$

Ta thấy, khi $m\in(0;3)$ thì đường thẳng $y=m$ luôn cắt hai đồ thị $y=-x^2$ và $y=-x^2+3$ tại $2$ điểm phân biệt khác $0$, tức là phương trình $g'(x)=0$ có $3$ nghiệm phân biệt.
