Ngân hàng bài tập
B
Cho hình vuông $ABCD$ tâm $O$. Gọi $M,\,N,\,P,\,Q$ lần lượt là trung điểm của các cạnh $AB$, $BC$, $CD$, $DA$.
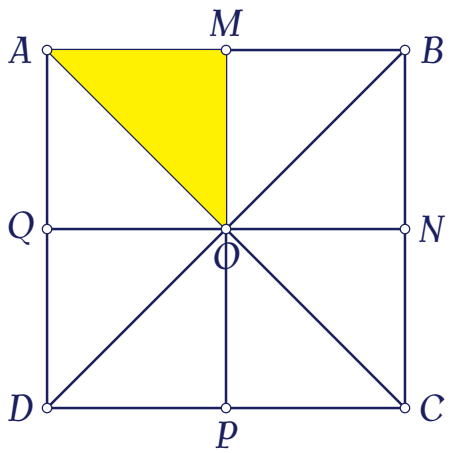
Ảnh của tam giác $OAM$ qua phép quay tâm $O$ góc $90^\circ$ là
| $\triangle ODQ$ | |
| $\triangle OBN$ | |
| $\triangle OAQ$ | |
| $\triangle OCN$ |
1 lời giải
Chọn phương án A.
Theo hình vẽ ta có $\begin{cases}
\mathrm{Q}_{(O,90^\circ)}(O)=O\\
\mathrm{Q}_{(O,90^\circ)}(A)=D\\
\mathrm{Q}_{(O,90^\circ)}(M)=Q
\end{cases}$
Vậy ảnh của tam giác $OAM$ qua phép quay tâm $O$ góc $90^\circ$ là tam giác $ODQ$.
