Ngân hàng bài tập
SS
Cho hàm số bậc hai $y=f(x)$ có đồ thị như hình vẽ.
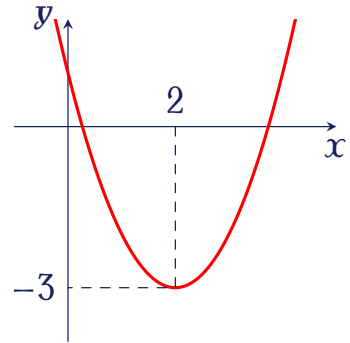
Tìm số nghiệm thực của phương trình $\big|f\big(x^3-2x^2+x\big)\big|=2$.
| $1$ | |
| $3$ | |
| $4$ | |
| $2$ |
1 lời giải
Chọn phương án C.
Đặt $g(x)=f\big(x^3-2x^2+x\big)$.
Ta có $g'(x)=\big(3x^2-4x+1\big)f'\big(x^3-2x^2+x\big)$.
Cho $g'(x)=0\Leftrightarrow\left[\begin{array}{l}3x^2-4x+1=0\\ f'\big(x^3-2x^2+x\big)=0\end{array}\right.$
- $3x^2-4x+1=0\Leftrightarrow\left[\begin{array}{l}x=1\\ x=\dfrac{1}{3}\end{array}\right.$
- $f'\big(x^3-2x^2+x\big)=0\Leftrightarrow x^3-2x^2+x=2\Leftrightarrow x=2$.
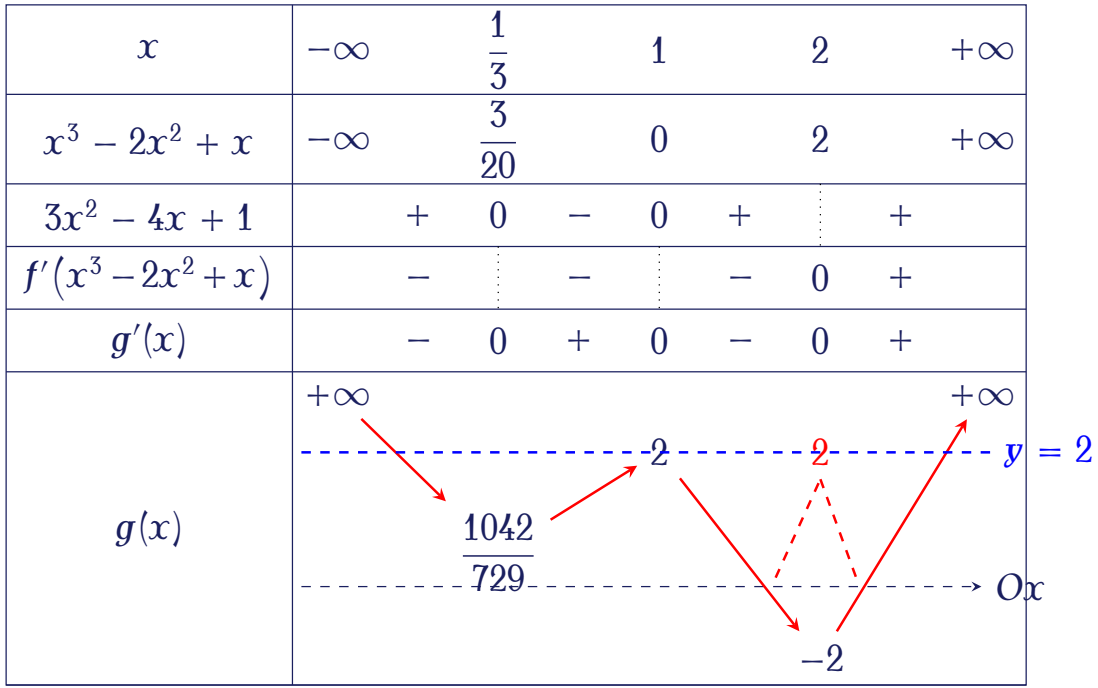
Ta thấy đường thẳng $y=2$ cắt đồ thị hàm số $y=\big|f\big(x^3-2x^2+x\big)\big|$ tại $4$ điểm nên phương trình đã cho có $4$ nghiệm.
