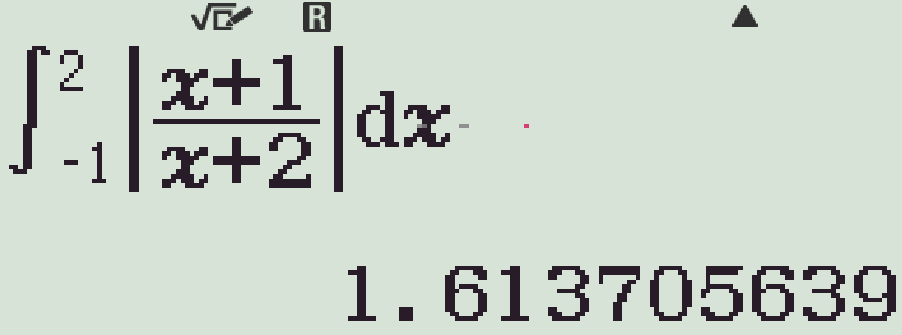Ngân hàng bài tập
A
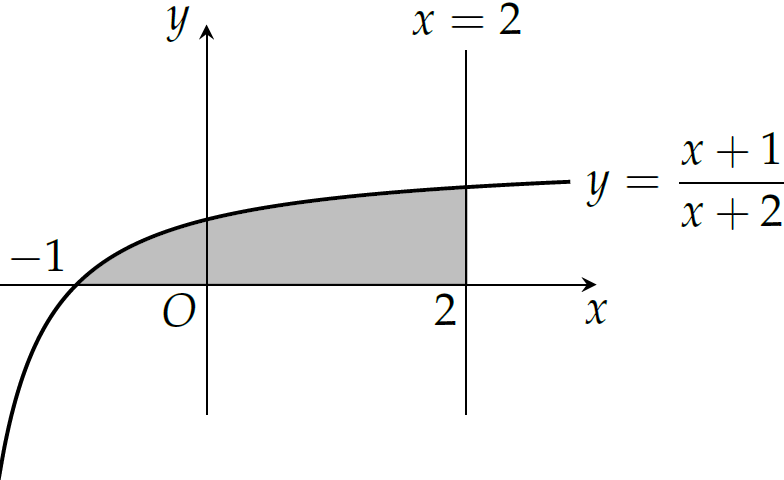
Diện tích hình phẳng được giới hạn bởi đồ thị hàm số \(y=\dfrac{x+1}{x+2}\), trục hoành và đường thẳng \(x=2\) là
| \(3+\ln2\) | |
| \(3-\ln2\) | |
| \(3+2\ln2\) | |
| \(3-2\ln2\) |
1 lời giải
Chọn phương án D.
Phương trình hoành độ giao điểm: $$\dfrac{x+1}{x+2}=0\Leftrightarrow x=-1.$$
Bảng xét dấu:
Ta có: $$\begin{aligned}
\displaystyle S&=\,\int\limits_{-1}^2\left|\dfrac{x+1}{x+2}\right|\mathrm{\,d}x=\int\limits_{-1}^2\dfrac{x+1}{x+2}\mathrm{\,d}x\\
&=\,\int\limits_{-1}^2\left(1-\dfrac{1}{x+2}\right)\mathrm{\,d}x\\
&=\left(x-\ln|x+2|\right)\bigg|_{-1}^2\\
&=3-2\ln2.\end{aligned}$$