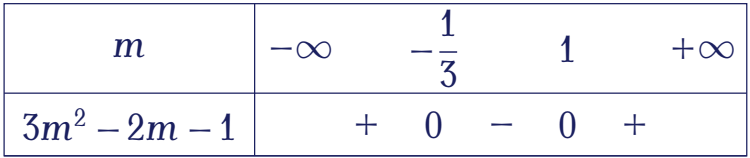Ngân hàng bài tập
A
Tìm tất cả các giá trị của tham số $\mathrm{m}$ để phương trình $\sin x+(m-1)\cos x=2m-1$ có nghiệm.
| $\dfrac{1}{3}\leqslant m\leqslant\dfrac{1}{2}$ | |
| $-\dfrac{1}{2}\leqslant m\leqslant\dfrac{1}{3}$ | |
| $-\dfrac{1}{3}\leqslant m\leqslant1$ | |
| $\dfrac{1}{2}\leqslant m\leqslant1$ |
1 lời giải
Chọn phương án C.
Phương trình đã cho có nghiệm khi $$\begin{aligned}
1^2+(m-1)^2\geq(2m-1)^2&\Leftrightarrow3m^2-2m-1\leq0\\
&\Leftrightarrow m\in\left[-\dfrac{1}{3};1\right].
\end{aligned}$$