Ngân hàng bài tập
SS
Tìm $m$ để phương trình $\dfrac{2\sin x+\cos x+1}{\sin x-2\cos x+3}=m$ có nghiệm.
| $\dfrac{1}{2}\leq m\leq2$ | |
| $m\geq2$ | |
| $m\leq-\dfrac{1}{2}$ | |
| $-\dfrac{1}{2}\leq m\leq2$ |
1 lời giải
Chọn phương án D.
Điều kiện: $\sin x-2\cos x+3\neq0$.
Phương trình đã cho trở thành
\begin{eqnarray*}
2\sin x+\cos x+1&=&m\sin x-2m\cos x+3m\\
\Leftrightarrow(2-m)\sin x+(1+2m)\cos x&=&3m-1.
\end{eqnarray*}
Phương trình trên có nghiệm khi
\begin{eqnarray*}
(2-m)^2+(1+2m)^2&\geq&(3m-1)^2\\
\Leftrightarrow2m^2-3m-2&\leq&0.
\end{eqnarray*}
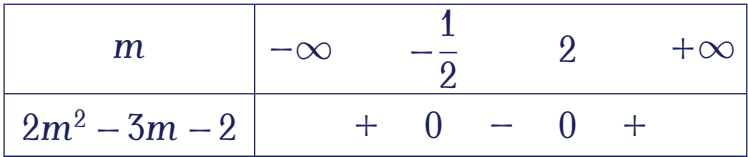
Vậy phương trình đã cho có nghiệm khi $-\dfrac{1}{2}\leq m\leq2$.
