Ngân hàng bài tập
S
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $I$ là trung điểm $SA$. Thiết diện của hình chóp $S.ABCD$ cắt bởi $(IBC)$ là
| Tam giác $IBC$ | |
| Hình thang $IGBC$ ($G$ là trung điểm $SB$) | |
| Hình thang $IJCB$ ($J$ là trung điểm $SD$) | |
| Tứ giác $IBCD$ |
1 lời giải
Chọn phương án C.
Dễ thấy $I$ là điểm chung của hai mặt phẳng $(IBC)$ và $(SAD)$.
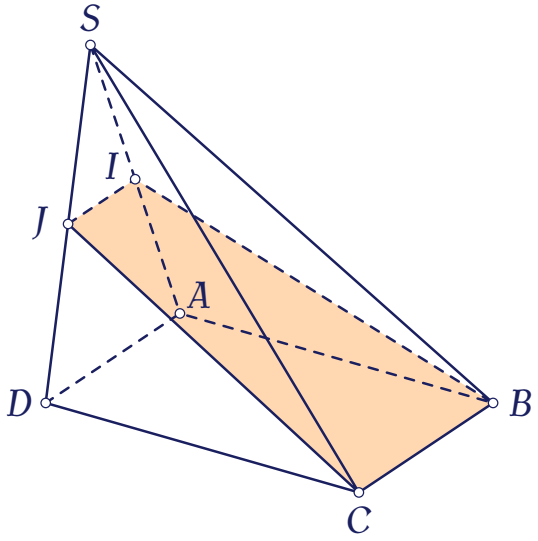
Ngoài ra, vì $BC\parallel AD$ nên giao tuyến của $(IBC)$ và $(SAD)$ là đường thẳng $\Delta$ đi qua $I$ và song song với $AD$.
Do đó, $\Delta$ là đường trung bình trong tam giác $SAD$.
Nói cách khác, $\Delta$ cắt $SD$ tại trung điểm $J$ của $SD$.
Vậy thiết diện của hình chóp cắt bởi mặt phẳng $(IBC)$ là hình thang $IJCB$, với $J$ là trung điểm cạnh $SD$.
