Ngân hàng bài tập
A
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình bình hành. Gọi $d$ là giao tuyến của hai mặt phẳng $(SAD)$ và $(SBC)$. Khẳng định nào sau đây đúng?
| $d$ qua $S$ và song song với $BC$ | |
| $d$ qua $S$ và song song với $DC$ | |
| $d$ qua $S$ và song song với $AB$ | |
| $d$ qua $S$ và song song với $BD$ |
1 lời giải
Chọn phương án A.
Dễ thấy $S$ là điểm chung của $(SAD)$ và $(SBC)$.
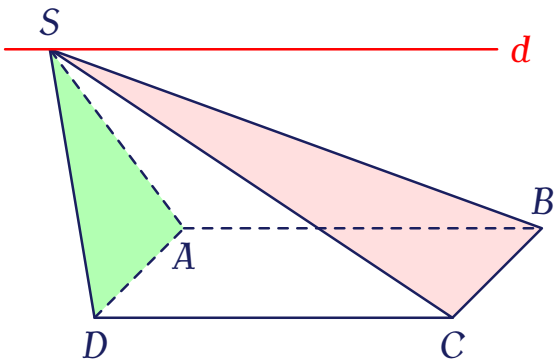
Vì $AD\parallel BC$ nên giao tuyến $d$ của $(SAD)$ và $(SBC)$ là đường thẳng qua $S$ và song song với $BC$.
