Ngân hàng bài tập
SS
Trong mặt phẳng $(\alpha)$, cho hình bình hành $ABCD$ tâm $O$, $S$ là một điểm không thuộc $(\alpha)$. Gọi $M,\,N,\,P$ lần lượt là trung điểm của $BC$, $CD$ và $SO$. Đường thẳng $MN$ cắt $AB$, $AC$ và $AD$ tại $M_1$, $N_1$ và $O_1$. Nối $N_1P$ cắt $SA$ tại $P_1$, nối $M_1P_1$ cắt $SB$ tại $M_2$, nối $O_1P_1$ cắt $SD$ tại $N_2$. Khi đó thiết diện của mặt phẳng $(MNP)$ với hình chóp $S.ABCD$ là
| Tam giác $MNP$ | |
| Tứ giác $BM_2N_2N$ | |
| Ngũ giác $NMM_2P_1N_2$ | |
| Tam giác $P_1M_1N_1$ |
1 lời giải
Chọn phương án C.
Mặt phẳng $(MNP)$ cắt mặt đáy $(ABCD)$ theo giao tuyến $MN$, cắt $(SCD)$ theo giao tuyến $NN_2$, cắt $(SDA)$ theo giao tuyến $N_2P_1$, cắt $(SAB)$ theo giao tuyến $P_1M_2$, cắt $(SBC)$ theo giao tuyến $M_2M$.
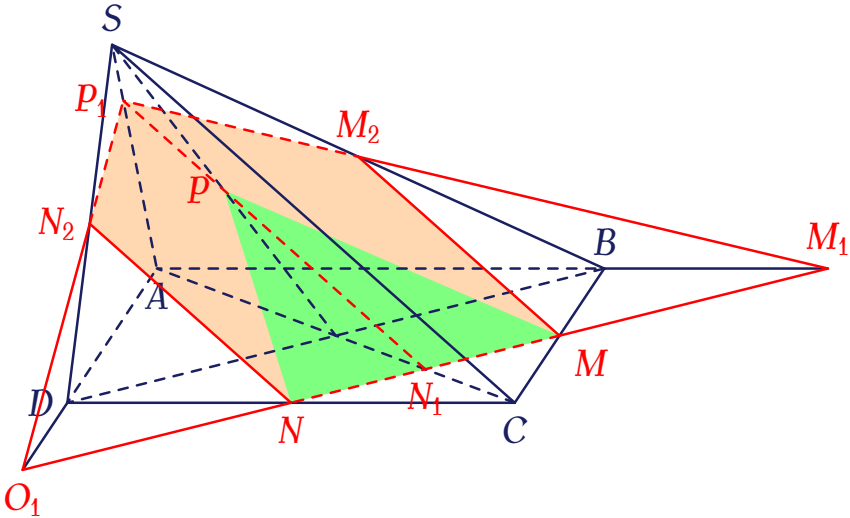
Vậy thiết diện là ngũ giác $NMM_2P_1N_2$.
