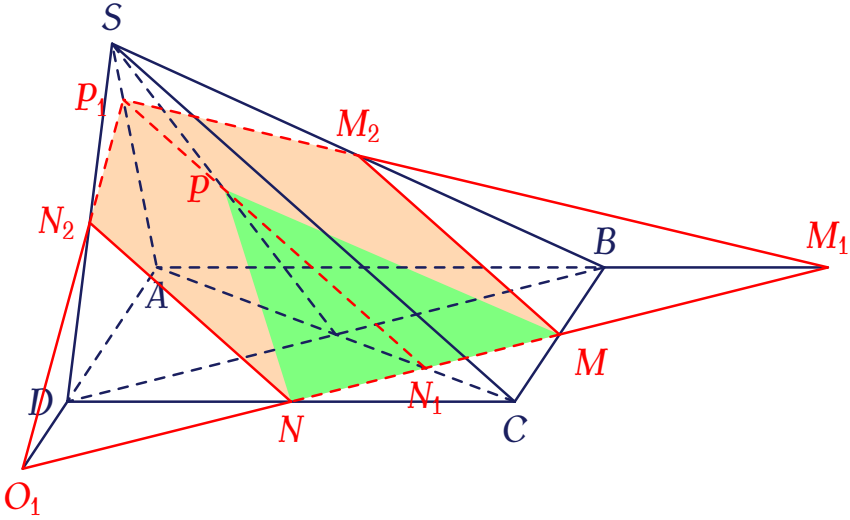
Trong mặt phẳng $(\alpha)$, cho hình bình hành $ABCD$ tâm $O$, $S$ là một điểm không thuộc $(\alpha)$. Gọi $M,\,N,\,P$ lần lượt là trung điểm của $BC$, $CD$ và $SO$. Đường thẳng $MN$ cắt $AB$, $AC$ và $AD$ tại $M_1$, $N_1$ và $O_1$. Nối $N_1P$ cắt $SA$ tại $P_1$, nối $M_1P_1$ cắt $SB$ tại $M_2$, nối $O_1P_1$ cắt $SD$ tại $N_2$. Khi đó giao tuyến của $(MNP)$ với $(SAB)$ là
| $P_1N_2$ | |
| $P_1M_2$ | |
| $P_1C$ | |
| $M_1N_1$ |
Chọn phương án B.
Ta có $\begin{cases}
P_1\in PN_1\\ P_1\in SA
\end{cases}\Rightarrow\begin{cases}
P_1\in(MNP)\\ P_1\in(SAB)
\end{cases}$
Suy ra $P_1$ là điểm chung của $(MNP)$ và $(SAB)$.
Lại có $\begin{cases}
M_2\in P_1M_1\\ M_2\in SB
\end{cases}\Rightarrow\begin{cases}
M_2\in(MNP)\\ M_2\in(SAB)
\end{cases}$
Suy ra $M_2$ là điểm chung của $(MNP)$ và $(SAB)$.
Vậy $P_1M_2$ là giao tuyến cần tìm.
