Ngân hàng bài tập
B
Trong $(\alpha)$, cho tứ giác $ABCD$ có $AB$ cắt $CD$ tại $E$, $AC$ cắt $BD$ tại $F$, $S$ là điểm không thuộc $(\alpha)$. Giao tuyến của $(SAB)$ và $(SCD)$ là
| $AC$ | |
| $SD$ | |
| $CD$ | |
| $SE$ |
1 lời giải
Chọn phương án D.
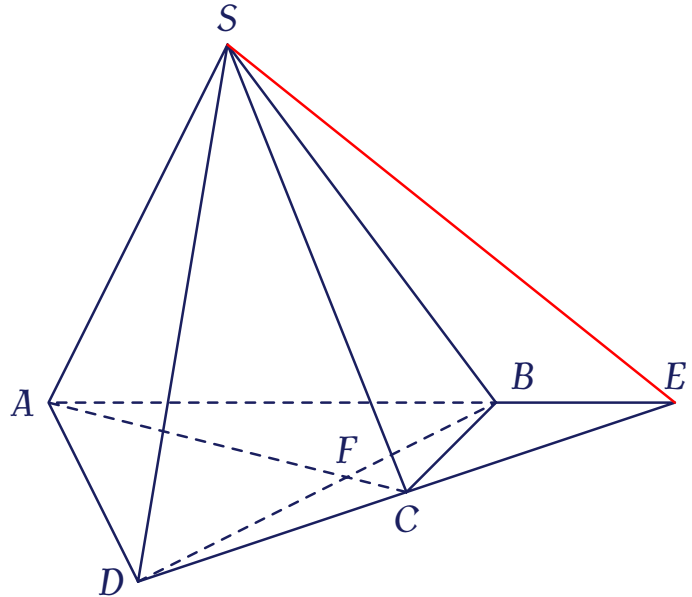
Dễ thấy $S$ là điểm chung của $(SAB)$ và $(SCD)$.
Lại có $\begin{cases}
E\in AB\\ E\in CD
\end{cases}\Rightarrow\begin{cases}
E\in(SAB)\\ E\in(SCD)
\end{cases}$
Suy ra $E$ là điểm chung của $(SAB)$ và $(SCD)$.
Vậy $SE$ là giao tuyến cần tìm.
