Ngân hàng bài tập
SS
Cho hàm số $f(x)=\left|x^4-4x^3+4x^2+a\right|$. Gọi $M,\,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn $[0;2]$. Có bao nhiêu số nguyên $a$ thuộc đoạn $[-3;2]$ sao cho $M\leq2m$?
| $7$ | |
| $5$ | |
| $6$ | |
| $4$ |
1 lời giải
Chọn phương án D.
Xét hàm số $g(x)=x^4-4x^3+4x^2+a$.
Ta có $g'(x)=4x^3-12x^2+8x$.
Cho $g'(x)=0\Leftrightarrow\left[\begin{array}{l}x=0\\ x=1\\ x=2.\end{array}\right.$
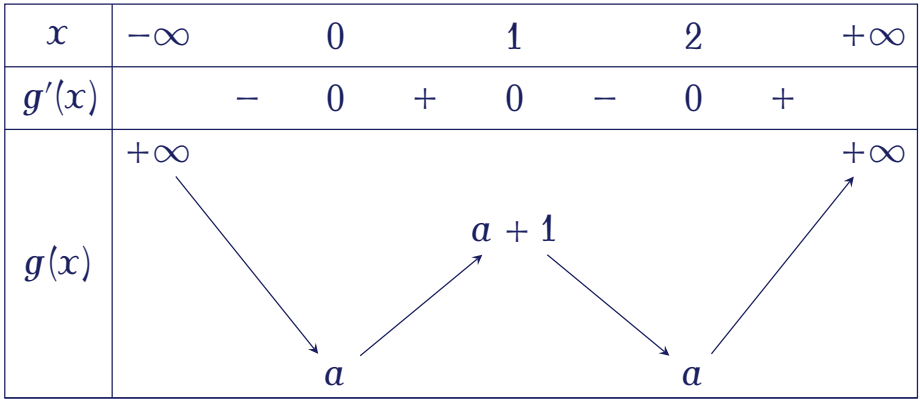
Với $M=\max\limits_{[0;2]}\big|g(x)\big|$ và $m=\min\limits_{[0;2]}\big|g(x)\big|$ ta có các trường hợp sau:
- Với $a\geq0$ ta có $\begin{cases}M=a+1\\ m=a.\end{cases}$
Khi đó $M\leq2m\Leftrightarrow a+1\leq2a\Leftrightarrow a\geq1$.
Vì $a$ nguyên và thuộc đoạn $[-3;2]$ nên $a\in\{1;2\}$. - Với $a+1\leq0\Leftrightarrow a\leq-1$ ta có $\begin{cases}M=-a\\ m=-a-1.\end{cases}$
Khi đó $M\leq2m\Leftrightarrow-a\leq-2a-2\Leftrightarrow a\leq-2$.
Vì $a$ nguyên và thuộc đoạn $[-3;2]$ nên $a\in\{-3;-2\}$. - Với $-1<a<0$ ta có $m=0$.
Khi đó $M\leq2m\Leftrightarrow M\leq0\Leftrightarrow M=0\Leftrightarrow\left[\begin{array}{ll}m=0 &\text{(loại)}\\ m=-1 &\text{(loại)}\end{array}\right.$.
Vậy có $4$ giá trị của $a$ thỏa đề.
