Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}\setminus\{-1\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình bên.

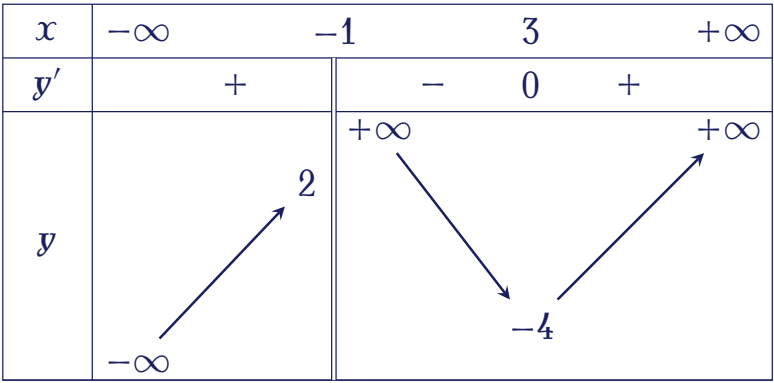
Tìm tập hợp tất cả các giá trị thực của tham số $m$ sao cho phương trình $f(x)=m$ có đúng ba nghiệm thực phân biệt.

	$(-4;2)$
	$[-4;2)$
	$(-4;2]$
	$(-\infty;2]$