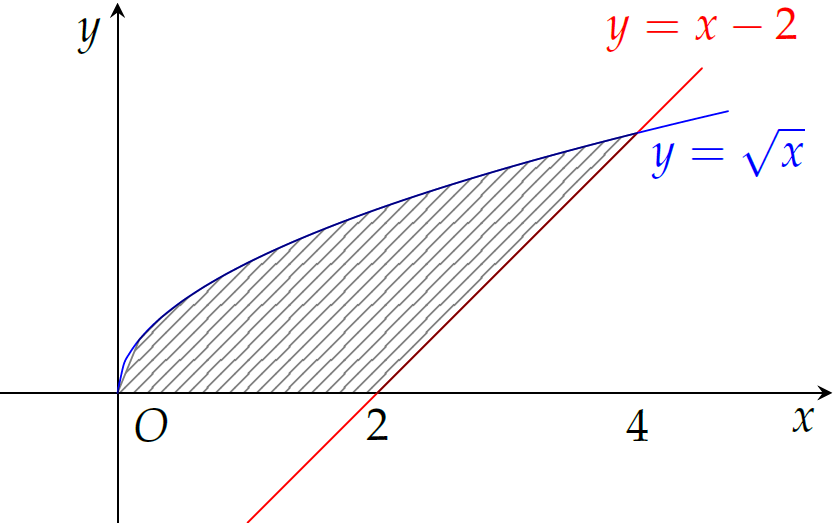
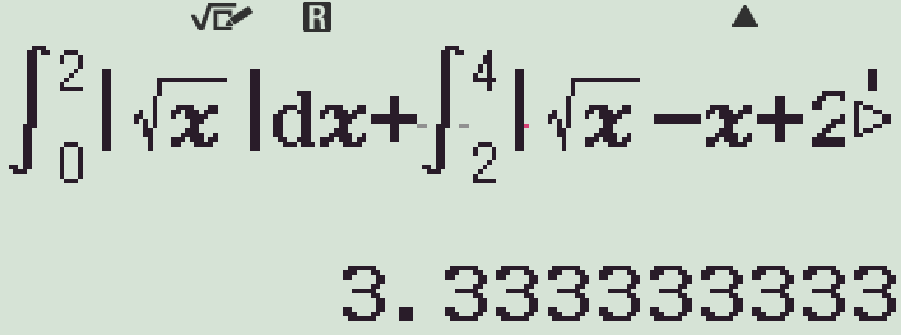Tính diện tích \(S\) của hình phẳng (phần gạch sọc) trong hình.
| \(S=\dfrac{8}{3}\) | |
| \(S=\dfrac{10}{3}\) | |
| \(S=\dfrac{11}{3}\) | |
| \(S=\dfrac{7}{3}\) |
Chọn phương án B.
Dựa vào hình vẽ, ta thấy hình phẳng được giới hạn bởi các đường \(\begin{cases}y=\sqrt{x}\\ y=x-2\\ y=0.\end{cases}\)
Do đó: $$\begin{aligned}
S&=S_1+S_2\\
&=\displaystyle\int\limits_0^2\left|\sqrt{x}-0\right|\mathrm{\,d}x+\displaystyle\int\limits_2^4\left|\sqrt{x}-(x-2)\right|\mathrm{\,d}x\\
&=\displaystyle\int\limits_0^2\sqrt{x}\mathrm{\,d}x+\displaystyle\int\limits_2^4\left(\sqrt{x}-x+2\right)\mathrm{\,d}x\\
&=\displaystyle\int\limits_0^2x^{\tfrac{1}{2}}\mathrm{\,d}x+\displaystyle\int\limits_2^4\left(x^{\tfrac{1}{2}}-x+2\right)\mathrm{\,d}x\\
&=\dfrac{2}{3}\sqrt{x^3}\bigg|_0^2+\left(\dfrac{2}{3}\sqrt{x^3}-\dfrac{x^2}{2}+2x\right)\bigg|_2^4\\
&=\dfrac{10}{3}.\end{aligned}$$