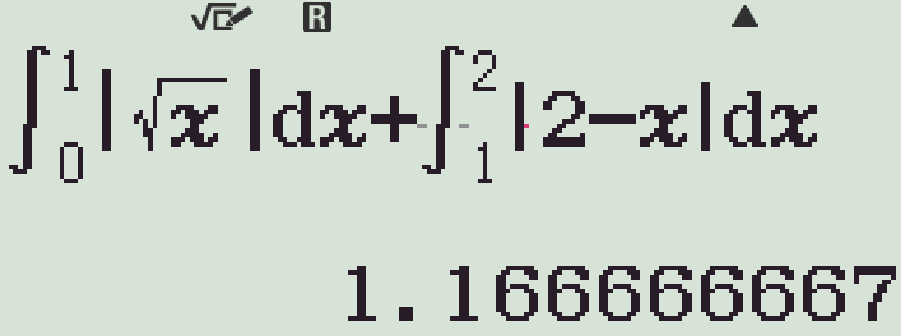Ngân hàng bài tập
A
Diện tích của hình phẳng giới hạn bởi các đường \(y=\sqrt{x}\), \(y=2-x\) và trục hoành bằng
| \(\dfrac{5}{6}\) | |
| \(\dfrac{5\pi}{6}\) | |
| \(\dfrac{7}{6}\) | |
| \(\dfrac{7\pi}{6}\) |
1 lời giải
Chọn phương án C.
Phương trình hoành độ giao điểm:
- \(\sqrt{x}=0\Leftrightarrow x=0\).
- \(\sqrt{x}=2-x\Leftrightarrow\begin{cases}2-x\geq0\\ x=4-4x+x^2\end{cases}\)
\(\Leftrightarrow\begin{cases}x\leq2\\ \left[\begin{array}{ll}x=1 &\text{(nhận)}\\ x=4 &\text{(loại)}\end{array}\right.\end{cases}\Leftrightarrow x=1\). - \(2-x=0\Leftrightarrow x=2\).
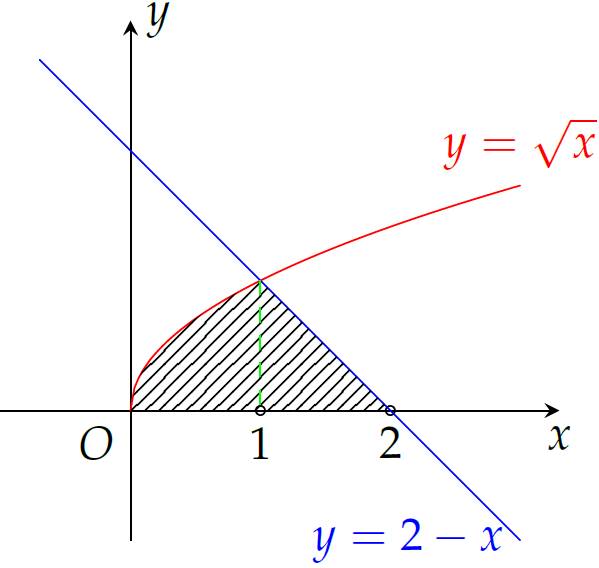
Khi đó: $$\begin{eqnarray*}
S&=&S_1+S_2\\
&=&\displaystyle\int\limits_0^1\left|\sqrt{x}-0\right|\mathrm{\,d}x+\displaystyle\int\limits_1^2\left|2-x-0\right|\mathrm{\,d}x\\
&=&\displaystyle\int\limits_0^1\sqrt{x}\mathrm{\,d}x+\displaystyle\int\limits_1^2\left(2-x\right)\mathrm{\,d}x\\
&=&\displaystyle\int\limits_0^1x^{\tfrac{1}{2}}\mathrm{\,d}x+\displaystyle\int\limits_1^2\left(2-x\right)\mathrm{\,d}x\\
&=&\dfrac{2}{3}\sqrt{x^3}\bigg|_0^1+\left(2x-\dfrac{x^2}{2}\right)\bigg|_1^2\\
&=&\dfrac{2}{3}+\dfrac{1}{2}=\dfrac{7}{6}.\end{eqnarray*}$$