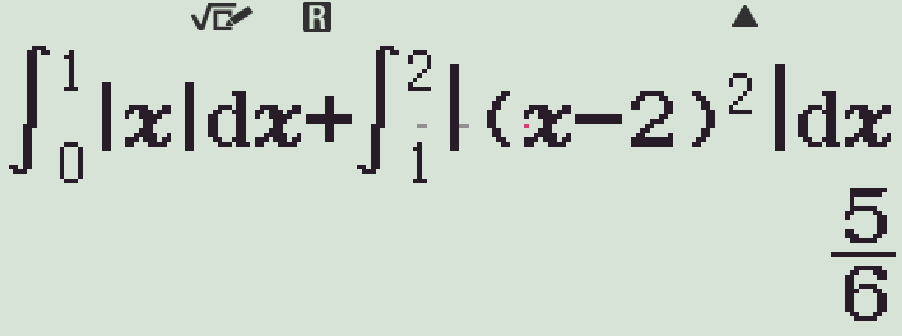Ngân hàng bài tập
A
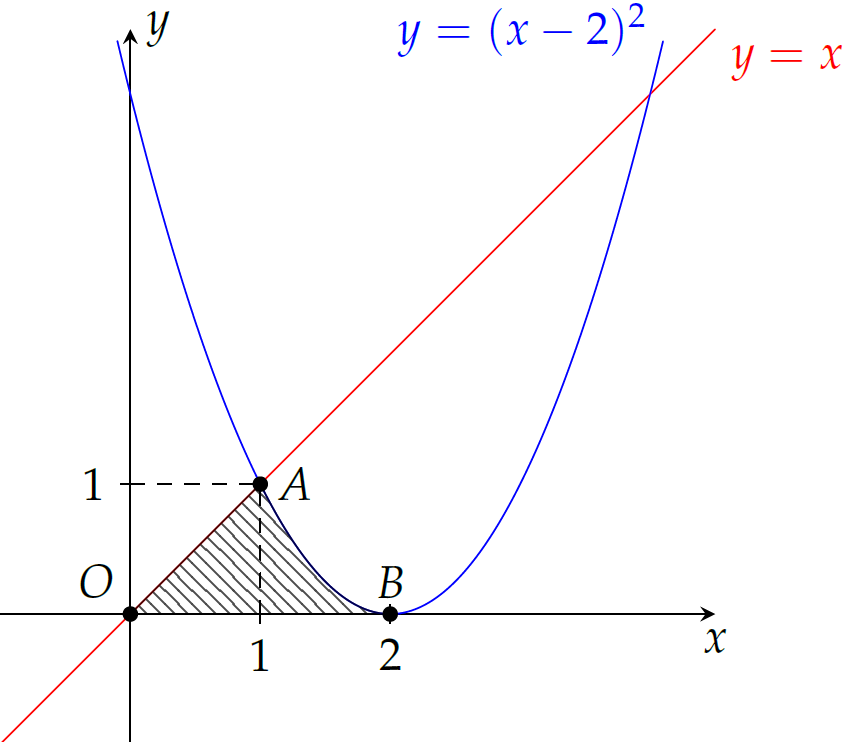
Tính diện tích phần hình phẳng gạch chéo (tam giác cong \(OAB\)) trong hình vẽ.
| \(\dfrac{5}{6}\) | |
| \(\dfrac{5\pi}{6}\) | |
| \(\dfrac{8}{15}\) | |
| \(\dfrac{8\pi}{15}\) |
1 lời giải
Chọn phương án A.
Theo hình vẽ, ta có: $$\begin{aligned}
S&=S_1+S_2\\
&=\displaystyle\int\limits_0^1|x-0|\mathrm{\,d}x+\int\limits_1^2\left|\left(x-2\right)^2-0\right|\mathrm{\,d}x\\
&=\displaystyle\int\limits_0^1x\mathrm{\,d}x+\int\limits_1^2\left(x-2\right)^2\mathrm{\,d}x\\
&=\dfrac{x^2}{2}\bigg|_0^1+\dfrac{(x-2)^3}{3}\bigg|_1^2\\
&=\dfrac{1}{2}+\dfrac{1}{3}=\dfrac{5}{6}.\end{aligned}$$