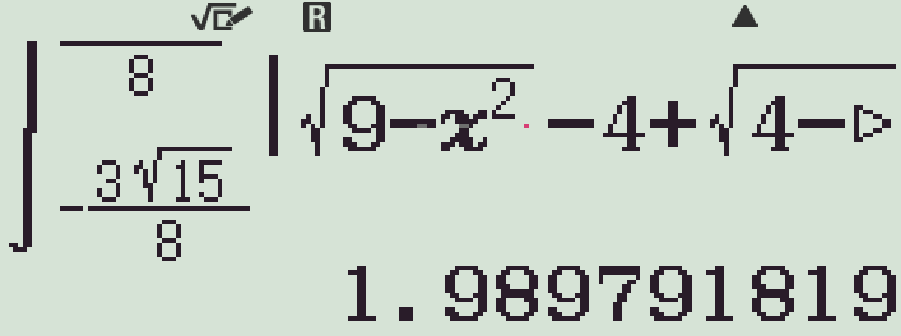Trên cánh đồng cỏ có hai con bò được cột vào hai cây cọc khác nhau. Biết khoảng cách giữa hai cọc là \(4\)m còn hai sợi dây cột hai con bò dài \(3\)m và \(2\)m. Tính phần diện tích mặt cỏ lớn nhất mà hai con bò có thể ăn chung (lấy giá trị gần đúng nhất).
| \(1,574\)m\(^2\) | |
| \(1,034\)m\(^2\) | |
| \(1,989\)m\(^2\) | |
| \(2,824\)m\(^2\) |
Chọn phương án C.
Giả sử con bò thứ nhất được cột vào cọc \(O(0;0)\) dây dài \(3\)m, con bò thứ hai được cột vào cọc \(B(0;4)\) dây dài \(2\) mét. Ta thấy:
- Con bò thứ nhất di chuyển trong hình tròn \(\left(C_1\right):x^2+y^2\leq9\).
- Con bò thứ hai di chuyển trong hình tròn \(\left(C_2\right):x^2+\left(y-4\right)^2\leq4\).
Ta có:
- \(x^2+(y-4)^2=4\)
\(\Leftrightarrow\left[\begin{array}{l}y=f_1(x)=4+\sqrt{4-x^2}\\ y=f_2(x)=4-\sqrt{4-x^2}.\end{array}\right.\) - \(x^2+y^2=9\)
\(\Leftrightarrow\left[\begin{array}{l}y=g_1(x)=\sqrt{9-x^2}\\ y=g_2(x)=-\sqrt{9-x^2}.\end{array}\right.\)
Giao điểm \(C\), \(D\) có tọa độ thỏa mãn $$f_2(x)=g_1(x)\Leftrightarrow\begin{cases}y=\dfrac{21}{8}\\ \left[\begin{array}{l}x=\dfrac{3\sqrt{15}}{8}\\ x=\dfrac{-3\sqrt{15}}{8}.\end{array}\right.\end{cases}$$
Suy ra \(C\left(-\dfrac{3\sqrt{15}}{8};\dfrac{21}{8}\right)\), \(D\left(\dfrac{3\sqrt{15}}{8};\dfrac{21}{8}\right)\).
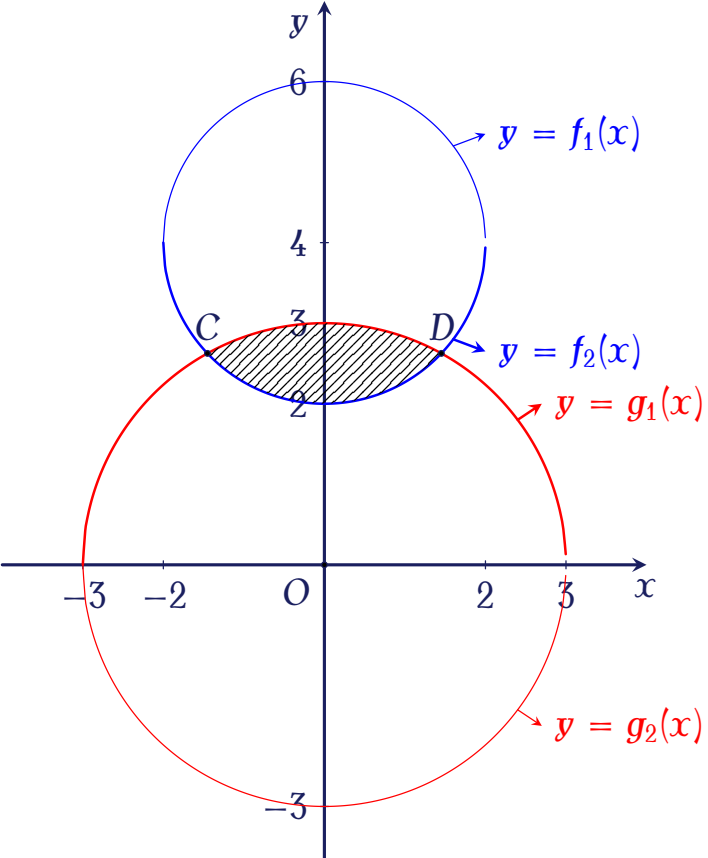
Diện tích phần giao nhau giữa hai đường tròn chính là diện tích phần cỏ lớn nhất mà hai con bò có thể ăn chung. Do đó: $$\begin{aligned}
S&=\displaystyle\int\limits_{-\tfrac{3\sqrt{15}}{8}}^{\tfrac{3\sqrt{15}}{8}}\left|g_1(x)-f_2(x)\right|\mathrm{\,d}x\\
&=\displaystyle\int\limits_{-\tfrac{3\sqrt{15}}{8}}^{\tfrac{3\sqrt{15}}{8}}\left|\sqrt{9-x^2}-\left(4-\sqrt{4-x^2}\right)\right|\mathrm{\,d}x\\
&=\displaystyle\int\limits_{-\tfrac{3\sqrt{15}}{8}}^{\tfrac{3\sqrt{15}}{8}}\left|\sqrt{9-x^2}-4+\sqrt{4-x^2}\right|\mathrm{\,d}x\\
&\approx 1.9898\text{m}^2.\end{aligned}$$