Ngân hàng bài tập
C
Cho hàm số $f(x)=ax^4+bx^2+c$ có đồ thị là đường cong trong hình bên.
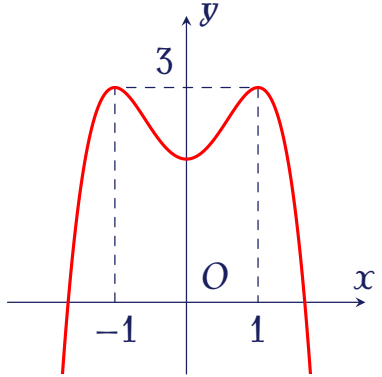
Số nghiệm thực của phương trình $f(x)=1$ là
| $1$ | |
| $2$ | |
| $4$ | |
| $3$ |
1 lời giải
Chọn phương án B.
Đường thẳng $y=1$ cắt đồ thị hàm số đã cho tại $2$ điểm phân biệt, tức là phương trình $f(x)=1$ có đúng $2$ nghiệm thực.
