Ngân hàng bài tập
S
Cho hình lăng trụ đứng $ABC.A'B'C'$ có đáy $ABC$ là tam giác vuông tại $B$, $AC=2$, $AB=\sqrt{3}$ và $AA'=1$ (tham khảo hình bên).
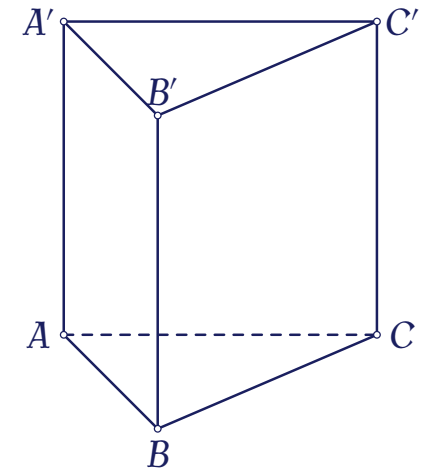
Góc giữa hai mặt phẳng $(ABC')$ và $(ABC)$ bằng
| $30^\circ$ | |
| $45^\circ$ | |
| $90^\circ$ | |
| $60^\circ$ |
1 lời giải
Chọn phương án B.

Ta có $\begin{cases}
AB=(ABC')\cap(ABC)\\
AB\perp BC'\,\big(AB\perp(BCC'B')\big)\\
AB\perp BC
\end{cases}$.
Suy ra $\big((ABC'),(ABC)\big)=(BC',BC)=\widehat{C'BC}$.
Xét tam giác $BCC'$ vuông tại $C$ ta có $$\tan\widehat{C'BC}=\dfrac{CC'}{BC}=\dfrac{AA'}{\sqrt{AC^2-AB^2}}=1.$$
Vậy $\widehat{C'BC}=45^\circ$.
