Ngân hàng bài tập
S
Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB=a$, $BC=2a$ và $AA'=3a$ (tham khảo hình bên).
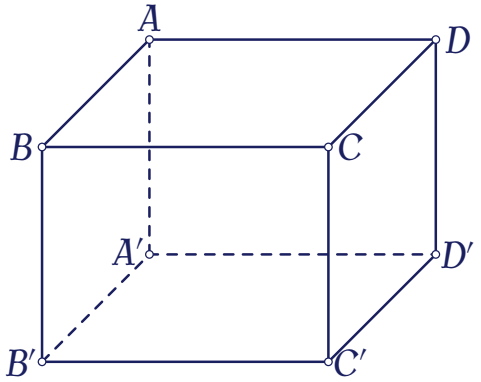
Khoảng cách giữa hai đường thẳng $BD$ và $A'C'$ bằng
| $a$ | |
| $a\sqrt{2}$ | |
| $2a$ | |
| $3a$ |
1 lời giải
Chọn phương án D.
Ta có $\begin{cases}
BD\subset(ABCD)\\
A'C'\subset(A'B'C'D')
\end{cases}$. Mà $(ABCD)\parallel(A'B'C'D')$, suy ra $$\mathrm{d}(BD,A'C')=\mathrm{d}\big((ABCD),(A'B'C'D')\big)=AA'=3a.$$
