Cho hình nón có góc ở đỉnh bằng $120^\circ$ và chiều cao bằng $4$. Gọi $(S)$ là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của $(S)$ bằng
| $64\pi$ | |
| $256\pi$ | |
| $192\pi$ | |
| $96\pi$ |
Chọn phương án B.
Giả sử hình nón có đỉnh $A$. Gọi $I,\,H$ lần lượt là tâm của mặt cầu và tâm đường tròn đáy của hình nón.
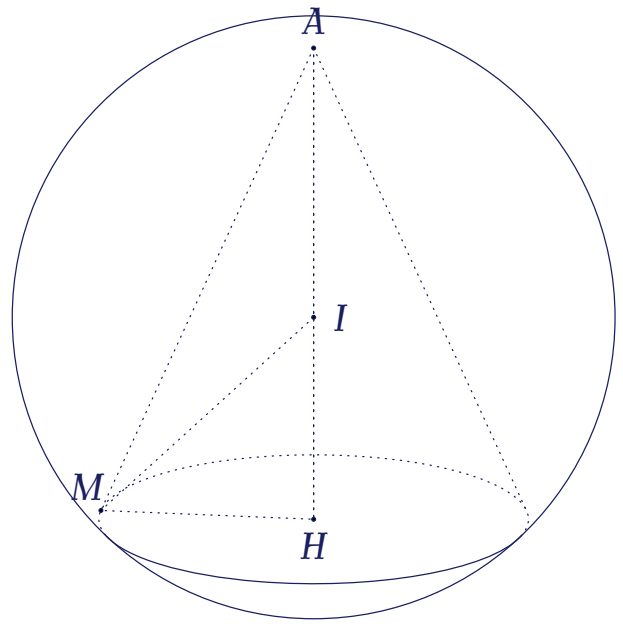
Xét điểm $M$ tùy ý trên đường tròn đáy của hình nón. Vì góc ở đỉnh của hình nón bằng $120^\circ$ nên $\widehat{HAM}=60^\circ$.
Trong tam giác vuông $HAM$ ta có $$\cos\widehat{HAM}=\dfrac{AH}{AM}\Rightarrow AM=\dfrac{AH}{\cos\widehat{HAM}}=\dfrac{4}{\cos60^\circ}=8.$$
Xét tam giác $AIM$ cân tại $I$, có $\widehat{HAM}=60^\circ$ và $AM=8$. Dễ thấy $\widehat{AIM}=180^\circ-\big(60^\circ+60^\circ\big)=60^\circ$, suy ra $\triangle AIM$ đều. Vậy $IM=IA=R=8$.
Do đó, diện tích của $(S)$ bằng $4\pi R^2=256\pi$.
