Cho các số phức $z_1,\,z_2,\,z_3$ thỏa mãn $\big|z_1\big|=\big|z_2\big|=2\big|z_3\big|=2$ và $8\big(z_1+z_2\big)z_3=3z_1z_2$. Gọi $A,\,B,\,C$ lần lượt là các điểm biểu diễn của $z_1,\,z_2,\,z_3$ trên mặt phẳng tọa độ. Diện tích tam giác $ABC$ bằng
| $\dfrac{\sqrt{55}}{32}$ | |
| $\dfrac{\sqrt{55}}{16}$ | |
| $\dfrac{\sqrt{55}}{24}$ | |
| $\dfrac{\sqrt{55}}{8}$ |
Chọn phương án B.
- Vì $\big|z_1\big|=\big|z_2\big|=2$ nên $A,\,B$ nằm trên đường tròn tâm $O$ bán kính bằng $2$.
- Vì $\big|z_3\big|=1$ nên điểm $C$ nằm trên đường tròn tâm $O$ bán kính bằng $1$.
$\begin{aligned}
8\big(z_1+z_2\big)z_3=3z_1z_2&\Leftrightarrow z_1+z_2=\dfrac{3z_1z_2}{8z_3}\\
&\Leftrightarrow\left|z_1+z_2\right|=\left|\dfrac{3z_1z_2}{8z_3}\right|=\dfrac{3\big|z_1\big|\cdot\big|z_2\big|}{8\big|z_3\big|}=\dfrac{3}{2}\\
&\Leftrightarrow\left|\overrightarrow{OA}+\overrightarrow{OB}\right|=\dfrac{3}{2}.
\end{aligned}$
Gọi $H$ là trung điểm của đoạn $AB$, ta có $\overrightarrow{OA}+\overrightarrow{OB}=2\overrightarrow{OH}$. Suy ra $$\left|2\overrightarrow{OH}\right|=\dfrac{3}{2}\Leftrightarrow OH=\dfrac{3}{4}.$$
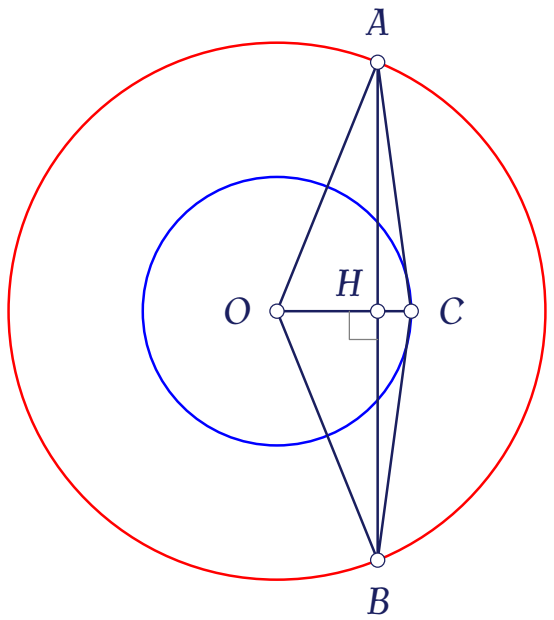
Khi đó $AH=\sqrt{OA^2-OH^2}=\sqrt{4-\dfrac{9}{16}}=\dfrac{\sqrt{55}}{4}$. Suy ra $AB=\dfrac{\sqrt{55}}{2}$ (1).
Từ $8\big(z_1+z_2\big)z_3=3z_1z_2$ ta cũng có $$\begin{aligned}
8z_1z_3+8z_2z_3=3z_1z_2&\Leftrightarrow16z_1z_3+16z_2z_3=3z_1z_2+3z_1z_2\\
&\Leftrightarrow\dfrac{16}{3}z_1z_3+\dfrac{16}{3}z_2z_3=z_1z_2+z_1z_2\\
&\Leftrightarrow z_1\left(\dfrac{16}{3}z_3-z_2\right)=z_2\left(z_1-\dfrac{16}{3}z_3\right)\\
&\Leftrightarrow\left|z_1\left(z_2-\dfrac{16}{3}z_3\right)\right|=\left|z_2\left(z_1-\dfrac{16}{3}z_3\right)\right|\\
&\Leftrightarrow\big|z_1\big|\cdot\left|z_2-\dfrac{16}{3}z_3\right|=\big|z_2\big|\cdot\left|z_1-\dfrac{16}{3}z_3\right|\\
&\Leftrightarrow\left|z_2-\dfrac{16}{3}z_3\right|=\left|z_1-\dfrac{16}{3}z_3\right|\,(2)
\end{aligned}$$
Gọi $C'$ là điểm biểu diễn của số phức $\dfrac{16}{3}z_3$. Từ (2) ta được $$\left|\overrightarrow{OB}-\overrightarrow{OC'}\right|=\left|\overrightarrow{OA}-\overrightarrow{OC'}\right|\Leftrightarrow\left|\overrightarrow{C'B}\right|=\left|\overrightarrow{C'A}\right|\Leftrightarrow C'B=C'A.$$
Suy ra $C'$ nằm trên đường trung trực của đoạn $AB$. Vì $\overrightarrow{OC'}$ và $\overrightarrow{OC}$ cùng hướng nên $C$ cũng nằm trên đường trung trực của đoạn $AB$. Nói cách khác, $O,\,H,\,C$ thẳng hàng.
Khi đó $CH=OC-OH=1-\dfrac{3}{4}=\dfrac{1}{4}$ (3).
Tam giác $ABC$ cân tại $C$ nên từ (1) và (3) ta suy ra $$S_{ABC}=\dfrac{1}{2}\cdot AB\cdot CH=\dfrac{1}{2}\cdot\dfrac{\sqrt{55}}{2}\cdot\dfrac{1}{4}=\dfrac{\sqrt{55}}{16}.$$
