Cho hàm số bậc bốn $y=f(x)$. Biết rằng hàm số $g(x)=\ln f(x)$ có bảng biến thiên như sau:
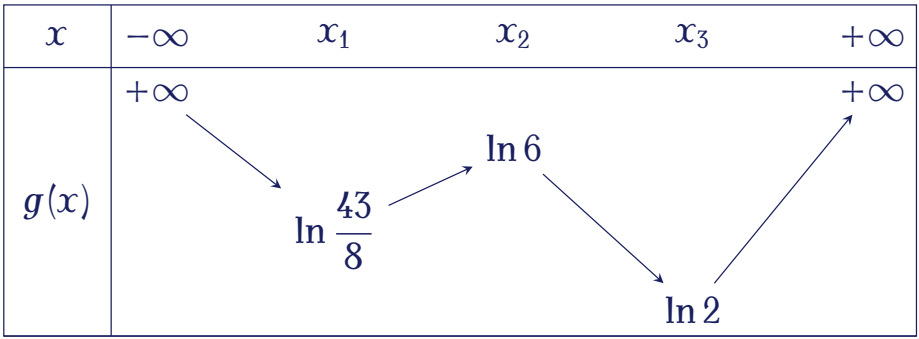
Diện tích hình phẳng giới hạn bởi các đường $y=f'(x)$ và $y=g'(x)$ thuộc khoảng nào dưới đây?
| $(5;6)$ | |
| $(4;5)$ | |
| $(2;3)$ | |
| $(3;4)$ |
Chọn phương án D.
Ta có $g(x)=\ln f(x)\Leftrightarrow f(x)=\mathrm{e}^{g(x)}$. Suy ra $f'(x)=g'(x)\cdot\mathrm{e}^{g(x)}$.
Phương trình hoành độ giao điểm: $$\begin{aligned}
f'(x)=g'(x)&\Leftrightarrow f'(x)-g'(x)=0\\
&\Leftrightarrow g'(x)\cdot\mathrm{e}^{g(x)}-g'(x)=0\\
&\Leftrightarrow g'(x)\left(\mathrm{e}^{g(x)}-1\right)=0\\
&\Leftrightarrow\left[\begin{array}{l}g'(x)=0\\ \mathrm{e}^{g(x)}-1=0\end{array}\right.\\
&\Leftrightarrow\left[\begin{array}{l}x=x_1\\ x=x_2\\ x=x_3\\ g(x)=0.\end{array}\right.
\end{aligned}$$
Dựa vào bảng biến thiên ta thấy $g(x)\geq\ln2>0$ nên phương trình $g(x)=0$ vô nghiệm.
Vậy $S=\displaystyle\int\limits_{x_1}^{x_3}\big|f'(x)-g'(x)\big|\mathrm{\,d}x=\displaystyle\int\limits_{x_1}^{x_3}\big|g'(x)\left(\mathrm{e}^{g(x)}-1\right)\big|\mathrm{\,d}x$.
- Vì $g(x)\geq\ln2$ nên $\mathrm{e}^{g(x)}\geq2\Leftrightarrow\mathrm{e}^{g(x)}-1\geq1$.
- $g'(x)>0$ trên khoảng $\big(x_1;x_2\big)$ và $g'(x)<0$ trên khoảng $\big(x_2;x_3\big)$
Suy ra $S=\displaystyle\int\limits_{x_1}^{x_2}\big[g'(x)\left(\mathrm{e}^{g(x)}-1\right)\big]\mathrm{\,d}x-\displaystyle\int\limits_{x_2}^{x_3}\big[g'(x)\left(\mathrm{e}^{g(x)}-1\right)\big]\mathrm{\,d}x$.
Đặt $u=g(x)$ ta có
- $\mathrm{d}u=g'(x)\mathrm{d}x$
- $x=x_1\Rightarrow u=g\big(x_1\big)=\ln\dfrac{43}{8}$
- $x=x_2\Rightarrow u=g\big(x_2\big)=\ln6$
- $x=x_3\Rightarrow u=g\big(x_3\big)=\ln2$
Suy ra $$\begin{aligned}
S&=\displaystyle\int\limits_{\ln\tfrac{43}{8}}^{\ln6}\big(\mathrm{e}^u-1\big)\mathrm{\,d}u-\displaystyle\int\limits_{\ln6}^{\ln2}\big(\mathrm{e}^u-1\big)\mathrm{\,d}u\\
&=\big(\mathrm{e}^u-x\big)\bigg|_{\ln\tfrac{43}{8}}^{\ln6}-\big(\mathrm{e}^u-x\big)\bigg|_{\ln6}^{\ln2}\\
&=\left(6-\ln6-\dfrac{43}{8}+\ln\dfrac{43}{8}\right)-\left(2-\ln2-6+\ln6\right)\\
&=\dfrac{37}{8}+\ln\dfrac{43}{144}\approx3,416\in(3;4).
\end{aligned}$$
