Trong không gian $Oxyz$, cho mặt cầu $(S)$ tâm $I(1;3;9)$ bán kính bằng $3$. Gọi $M,\,N$ là hai điểm lần lượt thuộc hai trục $Ox$, $Oz$ sao cho đường thẳng $MN$ tiếp xúc với $(S)$, đồng thời mặt cầu ngoại tiếp tứ diện $OIMN$ có bán kính bằng $\dfrac{13}{2}$. Gọi $A$ là tiếp điểm của $MN$ và $(S)$, giá trị $AM\cdot AN$ bằng
| $39$ | |
| $12\sqrt{3}$ | |
| $18$ | |
| $28\sqrt{3}$ |
Chọn phương án B.
Dễ thấy $\mathrm{d}\big(I,(Oxz)\big)=y_I=3=R$.
Suy ra mặt cầu $(S)$ tiếp xúc với mặt phẳng $(Oxz)$, cũng tức là mặt phẳng $(OMN)$.
Vì $A$ là tiếp điểm của $(S)$ với $MN$ nên $A$ cũng là tiếp điểm của $(S)$ với $(Oxz)$, suy ra $A$ là hình chiếu của tâm $I(1;3;9)$ trên mặt phẳng $(Oxz)$, ta được $A(1;0;9)$. Suy ra $IA=3$.
Giả sử $M(m;0;0)$, $N(0;0;n)$. Ta có $\overrightarrow{AM}=(m-1;0;-9)$, $\overrightarrow{AN}=(-1;0;n-9)$.
Vì $\overrightarrow{AM},\,\overrightarrow{AN}$ cùng phương nên $$\dfrac{m-1}{-1}=\dfrac{-9}{n-9}\Leftrightarrow(m-1)(n-9)=9\,(1)$$
Ta có $\begin{cases}
\overrightarrow{IM}=(m-1;-3;-9)\\
\overrightarrow{IN}=(-1;-3;9-n)
\end{cases}\Rightarrow\begin{cases}
IM=\sqrt{(m-1)^2+90}\\
IN=\sqrt{(n-9)^2+10}.
\end{cases}$
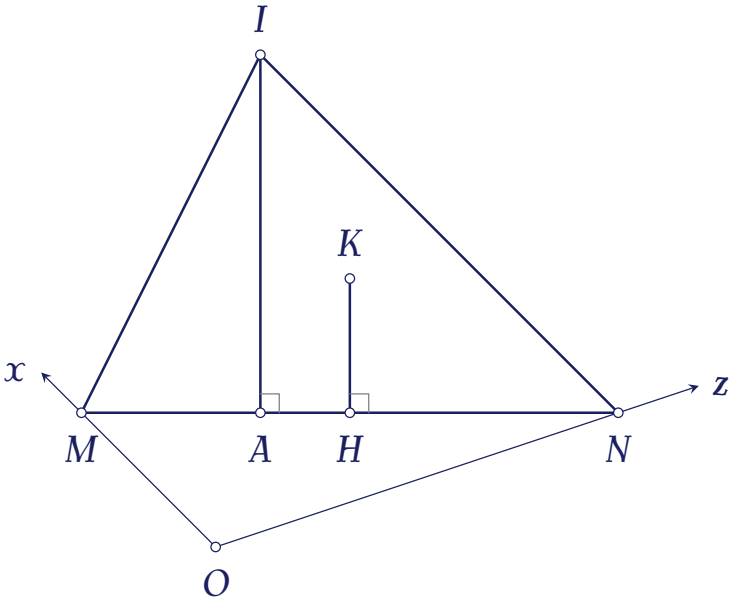
Vì $\triangle OMN$ vuông tại $O$ nên tâm đường tròn ngoại tiếp $\triangle OMN$ chính là trung điểm $H$ của cạnh huyền $MN$. Suy ra $KH\perp(OMN)$.
Như trên đã trình bày, $IA\perp(OMN)$. Vậy $K\in(IMN)$.
Vì $KI=KM=KN$ nên $K$ cũng là tâm đường tròn ngoại tiếp $\triangle IMN$.
Áp dụng định lý sin cho $\triangle IMN$ ta có $$\dfrac{IN}{\sin\widehat{IMN}}=2\cdot\dfrac{13}{2}=13\Rightarrow\sin\widehat{IMN}=\dfrac{IN}{13}.$$
Vì $\triangle IAM$ vuông tại $A$ nên $$\sin\widehat{IMN}=\dfrac{IA}{IM}=\dfrac{3}{IM}.$$
Vậy suy ra $\dfrac{IN}{13}=\dfrac{3}{IM}\Rightarrow IM\cdot IN=3\cdot13=39$, hay $$\sqrt{(m-1)^2+90}\cdot\sqrt{(n-9)^2+10}=39\,(2)$$
Đặt $\begin{cases}
u=(m-1)^2\\ n=(n-9)^2
\end{cases}$. Từ (1) và (2) ta có hệ $$\begin{aligned}
\begin{cases}
u\cdot v=9^2\\
\sqrt{u+90}\cdot\sqrt{v+10}=39
\end{cases}&\Leftrightarrow\begin{cases}
uv=81\\
(u+90)(v+10)=1521
\end{cases}\\
&\Leftrightarrow\begin{cases}
uv=81\\
uv+10u+90v=1521
\end{cases}\\
&\Leftrightarrow\begin{cases}
uv=81\\
10u+90v=540
\end{cases}\\
&\Leftrightarrow\begin{cases}
uv=81\\
u=54-9v
\end{cases}\\
&\Leftrightarrow\begin{cases}
(54-9v)v=81
u=54-9v
\end{cases}\\
&\Leftrightarrow\begin{cases}
u=27\\
v=3
\end{cases}
\end{aligned}$$
Vậy $AM\cdot AN=\sqrt{(m-1)^2+9^2}\cdot\sqrt{1^2+(n-9)^2}=\sqrt{u+81}\cdot\sqrt{1+v}=12\sqrt{3}$.
