Có bao nhiêu giá trị nguyên dương của tham số $m$ để hàm số $y=\big|x^4-2mx^2+64x\big|$ có đúng ba điểm cực trị?
| $5$ | |
| $6$ | |
| $12$ | |
| $11$ |
Chọn phương án C.
Xét hàm số $g(x)=x^4-2mx^2+64x=x\big(x^3-2mx+64\big)$.
Phương trình hoành độ giao điểm: $g(x)=0\Leftrightarrow\left[\begin{array}{ll}x=0\\
x^3-2mx+64=0 &(*)\end{array}\right.$
Phương trình bậc 3 (*) luôn có ít nhất một nghiệm, và vì $0^3-2m\cdot0+64\neq0$ nên các nghiệm ấy khác $0$.
Nói cách khác, đồ thị $g(x)$ luôn cắt trục hoành tại ít nhất hai điểm phân biệt.
Ngoài ra, $\lim\limits_{x\to\pm\infty}g(x)=\lim\limits_{x\to\pm\infty}\big(x^4-2mx^2+64x\big)=+\infty$.
Suy ra đồ thị $g(x)$ có ít nhất một điểm cực tiểu nằm phía dưới trục hoành.
Vậy đồ thị hàm số $y=\big|x^4-2mx^2+64x\big|$ có ít nhất $3$ điểm cực trị, bao gồm $2$ điểm cực tiểu và $1$ điểm cực đại.
Để đồ thị hàm số $y=\big|x^4-2mx^2+64x\big|$ có đúng $3$ điểm cực trị thì đồ thị hàm số $g(x)=x^4-2mx^2+64x$ có đúng một điểm cực tiểu, tức là phương trình $g'(x)=0$ có một nghiệm đơn.
Ta có $g'(x)=4x^3-4mx+64$.
Cho $g'(x)=0\Leftrightarrow x^3+16=mx$.
Với $x\neq0$, ta có $m=x^2+\dfrac{16}{x}$. Ta cần tìm $m$ sao cho đường thẳng $y=m$ cắt đồ thị $h(x)=x^2+\dfrac{16}{x}$ tại một điểm đơn.
Ta có $h'(x)=2x-\dfrac{16}{x^2}$. Cho $h'(x)=0\Leftrightarrow2x-\dfrac{16}{x^2}=0\Leftrightarrow x=2$.
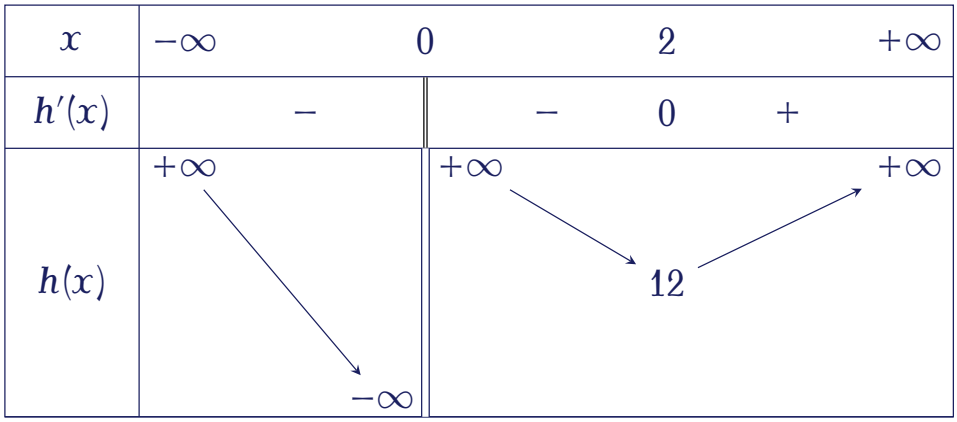
Từ bảng biến thiên ta suy ra $m\leq12$.
Vì $m\in\mathbb{Z}^+$ nên $m\in\{1;2;3;\ldots;11;12\}$, tức là có $12$ giá trị thỏa đề.
