Cho hình chóp $S.ABC$ có đáy là tam giác $ABC$ đều cạnh $a$. Hình chiếu của điểm $S$ trên mặt phẳng $(ABC)$ là điểm $H$ trên cạnh $AC$ thỏa mãn $AH=\dfrac{2}{3}AC$. Đường thẳng $SC$ tạo với mặt phẳng $(ABC)$ một góc bằng $60^\circ$. Thể tích của khối chóp $S.ABC$ bằng
| $\dfrac{a^3\sqrt{3}}{12}$ | |
| $\dfrac{a^3}{12}$ | |
| $\dfrac{a^3}{9}$ | |
| $\dfrac{a^3\sqrt{2}}{9}$ |
Chọn phương án B.
Vì $\triangle ABC$ đều cạnh $a$ nên có diện tích $S_{ABC}=\dfrac{a^2\sqrt{3}}{4}$.
Vì $SH\perp(ABC)$ nên $SH$ là đường cao của hình chóp.
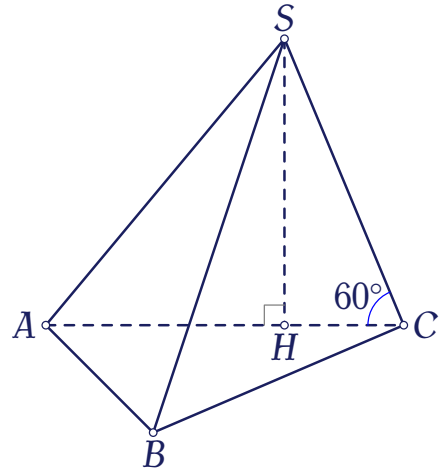
Ngoài ra, vì $HC$ là hình chiếu vuông góc của $SC$ trên mặt phẳng $(ABC)$ nên $$\big(SC,(ABC)\big)=(SC,HC)=\widehat{SCH}=60^\circ.$$
Tam giác $SHC$ vuông tại $H$ nên $$\tan\widehat{SCH}=\dfrac{SH}{HC}\Rightarrow SH=HC\cdot\tan\widehat{SCH}=\dfrac{a}{3}\cdot\sqrt{3}=\dfrac{a\sqrt{3}}{3}.$$
Vậy khối chóp đã cho có thể tích bằng $$V=\dfrac{1}{3}\cdot S_{ABC}\cdot SH=\dfrac{1}{3}\cdot\dfrac{a^2\sqrt{3}}{4}\cdot\dfrac{a\sqrt{3}}{3}=\dfrac{a^3}{12}.$$
