Ngân hàng bài tập
B
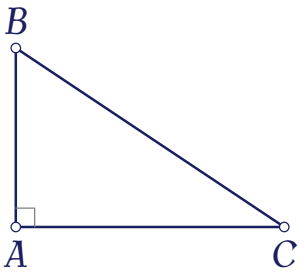
Trong không gian cho tam giác $ABC$ vuông tại $A$, $AB=2a$, $AC=3a$. Khi quay tam giác $ABC$ quanh cạnh $AB$ thì đường gấp khúc $ACB$ tạo thành một hình nón. Độ dài đường sinh của hình nón đó là
| $a\sqrt{13}$ | |
| $a\sqrt{5}$ | |
| $2a$ | |
| $3a$ |
1 lời giải
Chọn phương án A.
Khi quay tam giác $ABC$ quanh cạnh $AB$ thì đường gấp khúc $ACB$ tạo thành một hình nón có chiều cao $h=AB=2a$, bán kính đáy $r=AC=3a$.
Vậy đường sinh $$\ell=\sqrt{h^2+r^2}=\sqrt{4a^2+9a^2}=a\sqrt{13}.$$
