Ngân hàng bài tập
S
Cho hình trụ có bán kính đáy và chiều cao đều bằng $a$. Gọi $AB$, $CD$ là các dây cung của hai đường tròn đáy sao cho tứ giác $ABCD$ là hình vuông và mặt phẳng $ABCD$ không vuông góc với mặt phẳng đáy. Tính độ dài đoạn thẳng $AB$.
| $\dfrac{a\sqrt{5}}{3}$ | |
| $\dfrac{a\sqrt{5}}{2}$ | |
| $\dfrac{a\sqrt{10}}{2}$ | |
| $\dfrac{a\sqrt{10}}{3}$ |
1 lời giải
Chọn phương án C.
Gọi $C',D'$ lần lượt là hình chiếu vuông góc của $C,D$ trên đường tròn đáy chứa dây cung $AB$.
Dễ thấy tứ giác $CDD'C'$ là hình chữ nhật, do đó tứ giác $ABC'D'$ cũng là hình chữ nhật.
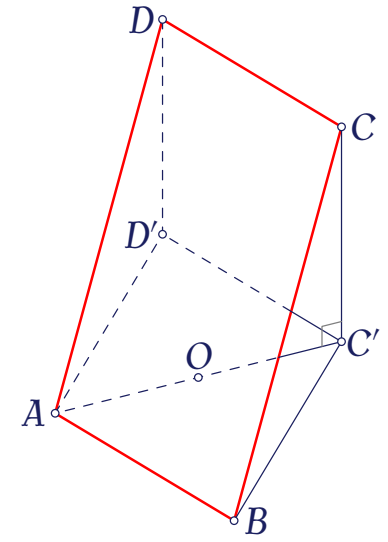
Tam giác $AC'C$ vuông tại $C'$, có $AC'=2r=2a$ và $CC'=h=a$. Suy ra $AC=\sqrt{AC'^2+C'C^2}=a\sqrt{5}$.
Vì $ABCD$ là hình vuông, có $AC$ là đường chéo nên cạnh $AB=\dfrac{AC}{\sqrt{2}}=\dfrac{a\sqrt{10}}{2}$.
