Ngân hàng bài tập
B
Cho khối lăng trụ đứng $ABC.A'B'C'$ có đáy là tam giác đều cạnh $a$ và $AA'=2a$ (minh họa như hình vẽ bên).
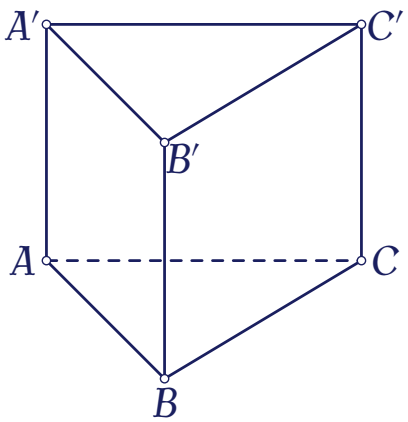
Thể tích của khối lăng trụ đã cho bằng
| $\sqrt{3}a^3$ | |
| $\dfrac{\sqrt{3}a^3}{6}$ | |
| $\dfrac{\sqrt{3}a^3}{3}$ | |
| $\dfrac{\sqrt{3}a^3}{2}$ |
1 lời giải
Chọn phương án D.
Diện tích đáy $S_{ABC}=\dfrac{a^2\sqrt{3}}{4}$.
Suy ra thể tích lăng trụ đã cho bằng $$V=S_{ABC}\cdot AA'=\dfrac{a^2\sqrt{3}}{4}\cdot2a=\dfrac{\sqrt{3}a^3}{2}.$$
