Từ một tấm tôn có kích thước $90\text{cm}\times300\text{cm}$, người ta làm một máng thoát nước, mặt cắt ngang của máng là hình thang cân $ABCD$ có đáy lớn $AD$, $AB=BC=CD=30$cm (hình minh họa bên).
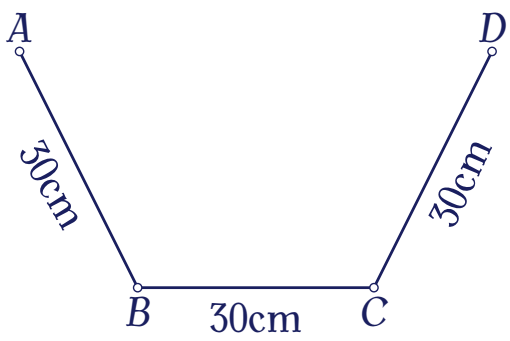
Thể tích lớn nhất của máng bằng
| $40500\sqrt{2}\text{cm}^3$ | |
| $40500\sqrt{5}\text{cm}^3$ | |
| $40500\sqrt{6}\text{cm}^3$ | |
| $202500\sqrt{3}\text{cm}^3$ |
Chọn phương án D.
Gọi $x$ (nhọn) là số đo góc $\widehat{BAH}$. Khi đó:
- $BH=AB\cdot\sin x=30\sin x$,
- $AH=AB\cdot\cos x=30\cos x$,
- $AD=HK+2AH=30+60\cos x$

Khi đó diện tích mặt cắt là $$\begin{aligned}
S&=\dfrac{1}{2}(BC+AD)\cdot BH\\
&=\dfrac{1}{2}\cdot30\sin x\big(30+30+60\cos x\big)\\
&=900(\sin x+\sin x\cos x)\\
&=900\left(\sin x+\dfrac{\sin2x}{2}\right).
\end{aligned}$$
Đặt $f(x)=\sin x+\dfrac{\sin2x}{2}$ ta có $f'(x)=\cos x+\cos2x$.
Cho $\begin{aligned}[t]
f'(x)=0&\Leftrightarrow\cos x+\cos2x=0\\
&\Leftrightarrow\cos x+2\cos^2x-1=0\\
&\Leftrightarrow\left[\begin{array}{l}\cos x=-1\\ \cos x=\dfrac{1}{2}\end{array}\right.\\
&\Leftrightarrow\left[\begin{array}{ll}x=\pi &\text{(loại)}\\ x=\dfrac{\pi}{3} &\text{(nhận)}.\end{array}\right.
\end{aligned}$

Vậy $f(x)$ đạt giá trị lớn nhất khi $x=\dfrac{\pi}{3}$.
Khi đó $S_{\text{max}}=900\left(\sin\dfrac{\pi}{3}+\sin\dfrac{\pi}{3}\cos\dfrac{\pi}{3}\right)=675\sqrt{3}\text{cm}^2$.
Vậy thể tích lớn nhất của máng là $300S_{\text{max}}=202500\sqrt{3}\text{cm}^3$.
