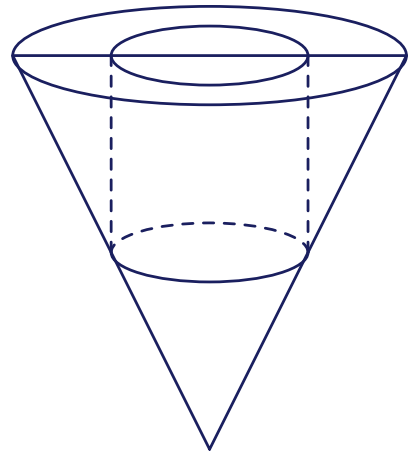
Một bình đựng nước dạng hình nón (không có nắp đậy), đựng đầy nước. Biết rằng chiều cao của bình gấp $3$ lần bán kính đáy của nó. Người ta thả vào bình đó một khối trụ và đo được thể tích nước tràn ra ngoài là $\dfrac{16\pi}{9}\text{dm}^3$. Biết rằng một mặt của khối trụ nằm trên mặt đáy của hình nón và khối trụ có chiều cao bằng đường kính đáy của hình nón (hình vẽ).
Tính bán kính đáy $R$ của bình nước.
| $R=4$dm | |
| $R=2$dm | |
| $R=3$dm | |
| $R=5$dm |
Chọn phương án B.
Theo đề bài ta có $V_{\text{nón}}=\dfrac{1}{3}\pi R^2\cdot3R=\pi R^3$.
Gọi $A$ là đỉnh của hình nón, $O$ và $O'$ là tâm đường tròn đáy của hình trụ, $B,\,B$ và $D$ là các điểm như hình vẽ.

Vì chiều cao của hình trụ bằng đường kính đáy của hình nón nên $OO'=2R$, suy ra $AO'=R$.
Xét hai tam giác đồng dạng $AOC$ và $AO'D$ ta có $$\dfrac{O'D}{OC}=\dfrac{AO'}{AO}=\dfrac{R}{3R}=\dfrac{1}{3}\Rightarrow O'D=\dfrac{OC}{3}=\dfrac{R}{3}.$$
Vì khối trụ có thể tích $\dfrac{16\pi}{9}\text{dm}^3$ nên $$\pi\left(\dfrac{R}{3}\right)^2\cdot2R=\dfrac{16\pi}{9}\Leftrightarrow R=2.$$
