Ngân hàng bài tập
S
Cho hàm số $y=f(x)$ có bảng xét dấu của $f'(x)$ như sau:
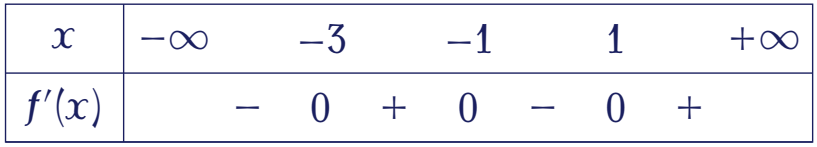
Hàm số $y=f(5-2x)$ đồng biến trên khoảng nào dưới đây?
| $(1;3)$ | |
| $(-\infty;-3)$ | |
| $(3;4)$ | |
| $(4;5)$ |
1 lời giải
Chọn phương án D.
Đặt $u=5-2x$. Ta có $y'=-2f'(u)$.
Cho $\begin{aligned}[t]
f'(u)=0&\Leftrightarrow\left[\begin{array}{l}u=-3\\ u=-1\\ u=1\end{array}\right.\\
&\Leftrightarrow\left[\begin{array}{l}5-2x=-3\\ 5-2x=-1\\ 5-2x=1\end{array}\right.\\
&\Leftrightarrow\left[\begin{array}{l}x=4\\ x=3\\ x=2\end{array}\right.
\end{aligned}$
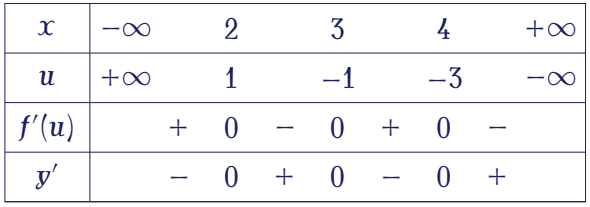
Dựa vào bảng biến thiên ta thấy hàm số $y=f(5-2x)$ đồng biến trên khoảng $(2;3)$ và $(4;+\infty)$ nên cũng đồng biến trên khoảng $(4;5)$.
