Cho hàm số $f(x)$, trong đó $f(x)$ là một đa giác. Hàm số $f'(x)$ có đồ thị như hình vẽ bên.
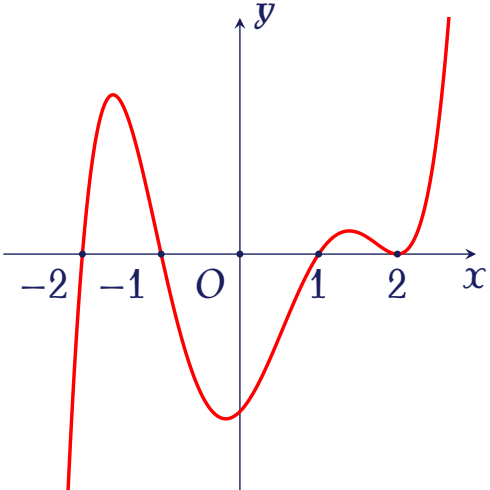
Hỏi có bao nhiêu giá trị nguyên $m$ thuộc $(-5;5)$ để hàm số $y=g(x)=f\big(x^2-2|x|+m\big)$ có $9$ điểm cực trị?
| $3$ | |
| $4$ | |
| $1$ | |
| $2$ |
Chọn phương án A.
Xét hàm số $h(x)=f\big(x^2-2x+m\big)$ với $x\geq0$.
Ta có $h'(x)=(2x-2)f'\big(x^2-2x+m\big)$.
Cho $\begin{aligned}[t]
h'(x)=0&\Leftrightarrow\left[\begin{array}{l}2x-2=0\\
f'\big(x^2-2x+m\big)=0\end{array}\right.\\
&\Leftrightarrow\left[\begin{array}{ll}x=1\\
x^2-2x+m=-2\\
x^2-2x+m=-1\\
x^2-2x+m=1\\
x^2-2x+m=2 &\text{(nghiệm kép)}
\end{array}\right.\\
&\Leftrightarrow\left[\begin{array}{l}x=1\\
m=-x^2+2x-2\\
m=-x^2+2x-1\\
m=-x^2+2x+1
\end{array}\right.
\end{aligned}$

Ta cần tìm $m$ sao cho đường thẳng $y=m$ cắt ba đường cong $f_1(x)=-x^2+2x-2$, $f_2(x)=-x^2+2x-1$, $f_3(x)=-x^2+2x+1$ tại $3$ điểm phân biệt.
Theo đồ thị ta thấy $m\in(-1;0)$ hoặc $m\leq-2$.
Vậy trên khoảng $(-5;5)$ có $3$ giá trị nguyên $m$ thỏa đề là $-2;-3;-4$.
