Ngân hàng bài tập
SS
Cho hàm số trùng phương $f(x)=ax^4+bx^2+c$ có đồ thị như hình vẽ.
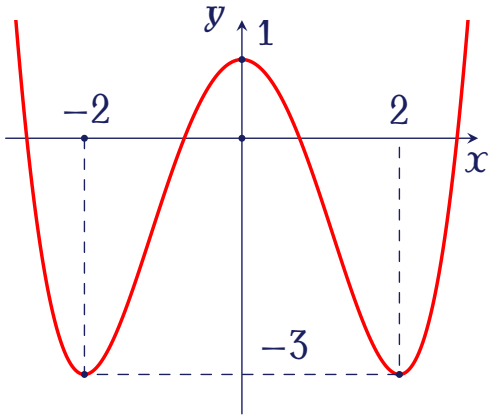
Hỏi đồ thị hàm số $y=\dfrac{2022}{\big[f(x)\big]^2+2f(x)-3}$ có tổng cộng bao nhiêu tiệm cận đứng?
| $4$ | |
| $3$ | |
| $5$ | |
| $2$ |
1 lời giải
Chọn phương án C.
Hàm số không xác định khi $$\big[f(x)\big]^2+2f(x)-3=0\Leftrightarrow\left[\begin{array}{l}f(x)=1\\ f(x)=-3\end{array}\right.$$
Dựa vào đồ thị $f(x)$ ta thấy
- Phương trình $f(x)=1$ có $3$ nghiệm $x=0$, $x=a$, $x=-a$
- Phương trình $f(x)=-3$ có $2$ nghiệm $x=\pm2$
Vậy hàm số $y=\dfrac{2022}{\big[f(x)\big]^2+2f(x)-3}$ có $5$ tiệm cận đứng.
