Ngân hàng bài tập
S
Cho hình chóp $S.ABC$ có $SA=SB=SC=AB=AC=10$, $BC=10\sqrt{2}$. Gọi $M$ là trung điểm của $BC$ và $\alpha$ là góc giữa $AM$ và $SB$. Tính $\cos\alpha$.
| $\cos\alpha=\dfrac{1}{3}$ | |
| $\cos\alpha=\dfrac{2}{5}$ | |
| $\cos\alpha=0$ | |
| $\cos\alpha=\dfrac{2}{3}$ |
1 lời giải
Chọn phương án C.
Gọi $N$ là trung điểm cạnh $SC$, dễ thấy $MN$ là đường trung bình của tam giác $SBC$, tức là $MN\parallel SB$.
Do đó $(AM,SB)=(AM,MN)=\widehat{AMN}$.
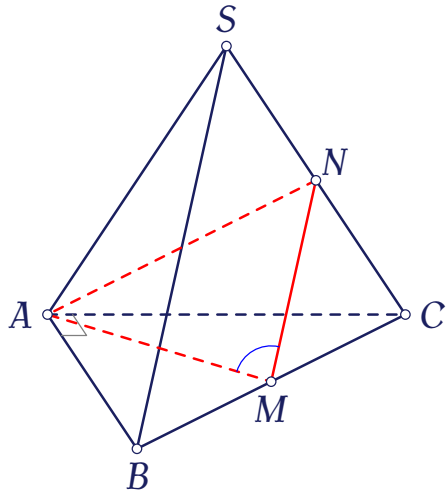
- $\triangle ABC$ vuông cân tại $A$ nên $AM=\dfrac{BC}{2}=5\sqrt{2}$.
- $MN$ là đường trung bình của $\triangle SBC$ nên $MN=\dfrac{SB}{2}=5$.
- $\triangle SAC$ đều nên $AN=SA\cdot\dfrac{\sqrt{3}}{2}=5\sqrt{3}$.
Vì $AM^2+MN^2=AN^2$ nên $\triangle AMN$ vuông tại $M$.
Vậy $\alpha=\widehat{AMN}=90^\circ$. Suy ra $\cos\alpha=0$.
