Ngân hàng bài tập
B
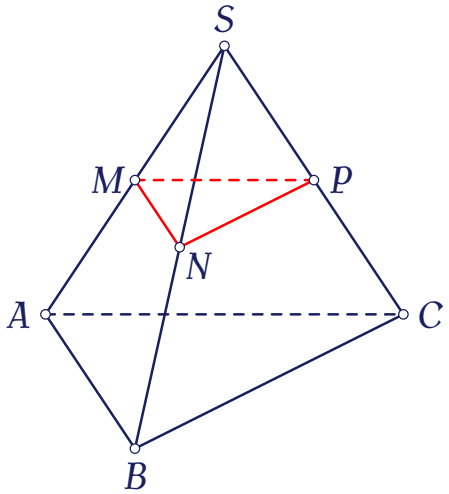
Cho hình chóp $S.ABC$. Gọi $M,\,N,\,P$ lần lượt là trung điểm của $SA,\,SB,\,SC$. Chọn khẳng định đúng.
| $(MNP)\parallel(ABC)$ | |
| $(MNP)\parallel(SAC)$ | |
| $(SMN)\parallel(ABC)$ | |
| $(MNP)\parallel(SBC)$ |
1 lời giải
Chọn phương án A.
Vì $\begin{cases}
MN\parallel(ABC)\\
NP\parallel(ABC)\\
MN,\,NP\subset(MNP)
\end{cases}$ nên $(MNP)\parallel(ABC)$.
