Ngân hàng bài tập
B
Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong trong hình bên.
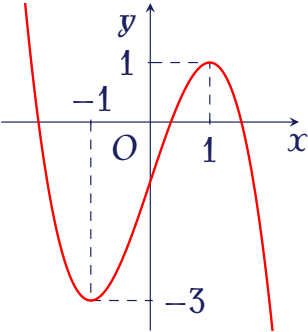
Có bao nhiêu giá trị nguyên của tham số $m$ để phương trình $f(x)=m$ có ba nghiệm thực phân biệt?
| $2$ | |
| $5$ | |
| $3$ | |
| $4$ |
1 lời giải
Chọn phương án C.
Theo đồ thị ta thấy phương trình $f(x)=m$ có ba nghiệm thực phân biệt khi $m\in(-3;1)$.
Vậy $m\in\{-2;-1;0\}$ thỏa đề.
