Cho hình chóp đều $S.ABCD$ có chiều cao $a$, $AC=2a$ (tham khảo hình bên).
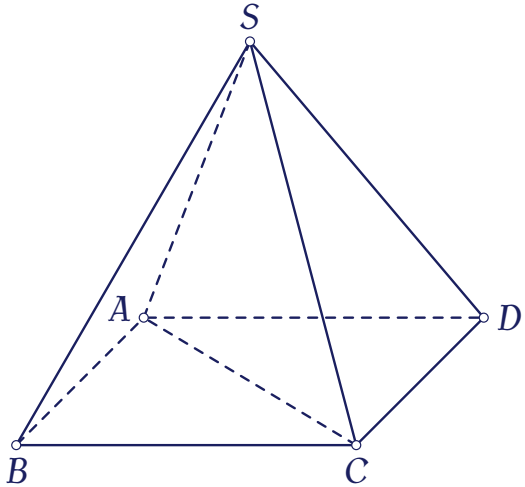
Khoảng cách từ $B$ đến mặt phẳng $(SCD)$ bằng
| $\dfrac{\sqrt{3}}{3}a$ | |
| $\sqrt{2}a$ | |
| $\dfrac{2\sqrt{3}}{3}a$ | |
| $\dfrac{\sqrt{2}}{2}a$ |
Chọn phương án C.
Gọi $H$ là giao điểm của $AC$ và $BD$, hay $H$ là trung điểm $BD$.
Vì $BD\cap(SCD)=D$ và $BD=2HD$ nên $\mathrm{d}\big(B,(SCD)\big)=2\mathrm{d}\big(H,(SCD)\big)$.
Gọi $M$ là trung điểm $CD$, gọi $HN$ là đường cao tam giác vuông $SHM$. Khi đó $HN\perp(SCD)$, tức là $\mathrm{d}\big(H,(SCD)\big)=HN$.

Hình chóp $S.ABCD$ có chiều cao $SH=a$ và cạnh đáy $BC=\dfrac{AC}{\sqrt{2}}=a\sqrt{2}$.
Khi đó $HM=\dfrac{BD}{2}=\dfrac{a\sqrt{2}}{2}$.
Xét tam giác vuông $SHM$ ta có $$\dfrac{1}{HN^2}=\dfrac{1}{HS^2}+\dfrac{1}{HM^2}=\dfrac{1}{a^2}+\dfrac{1}{\left(\dfrac{a\sqrt{2}}{2}\right)^2}=\dfrac{3}{a^2}$$
Suy ra $HN^2=\dfrac{a^2}{3}$ hay $HN=\dfrac{a\sqrt{3}}{3}$.
Vậy $\mathrm{d}\big(B,(SCD)\big)=2HN=\dfrac{2a\sqrt{3}}{3}$.
