Ngân hàng bài tập
A
Trong không gian $Oxyz$, cho mặt cầu $(S)\colon(x+3)^2+y^2+(z-1)^2=10$. Mặt phẳng nào trong các mặt phẳng dưới đây cắt mặt cầu $(S)$ theo giao tuyến là đường tròn có bán kính bằng $3$?
| $\big(P_2\big)\colon x+2y-2z-8=0$ | |
| $\big(P_4\big)\colon x+2y-2z-4=0$ | |
| $\big(P_3\big)\colon x+2y-2z-2=0$ | |
| $\big(P_1\big)\colon x+2y-2z+8=0$ |
1 lời giải
Chọn phương án D.
Mặt cầu $(S)$ có tâm $I(-3;0;1)$ và bán kính $R=\sqrt{10}$.
Giả sử mặt phẳng cắt mặt cầu theo giao tuyến là đường tròn như hình vẽ.
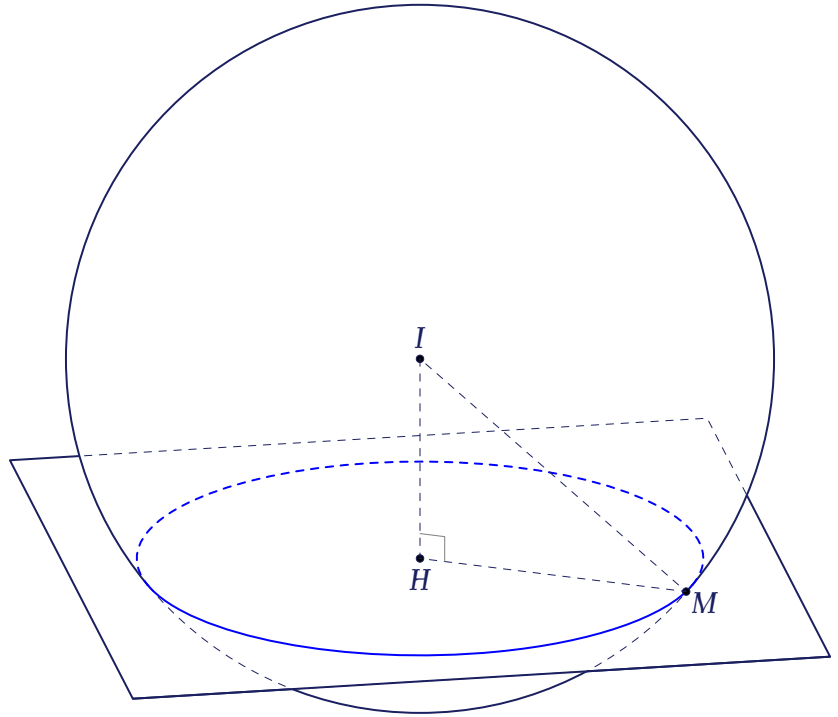
Theo yêu cầu đề bài thì $IH=\sqrt{HM^2-IH^2}=\sqrt{\sqrt{10}^2-3^2}=1$.
- $\mathrm{d}\left(I,\big(P_1\big)\right)=\dfrac{|-3+2\cdot0-2\cdot1+8|}{\sqrt{1^2+2^2+(-2)^2}}=1$;
- $\mathrm{d}\left(I,\big(P_2\big)\right)=\dfrac{|-3+2\cdot0-2\cdot1-8|}{\sqrt{1^2+2^2+(-2)^2}}=\dfrac{13}{3}$;
- $\mathrm{d}\left(I,\big(P_3\big)\right)=\dfrac{|-3+2\cdot0-2\cdot1-2|}{\sqrt{1^2+2^2+(-2)^2}}=\dfrac{7}{3}$;
- $\mathrm{d}\left(I,\big(P_4\big)\right)=\dfrac{|-3+2\cdot0-2\cdot1-4|}{\sqrt{1^2+2^2+(-2)^2}}=3$;
Vậy $\big(P_1\big)\colon x+2y-2z+8=0$ là mặt phẳng thỏa đề.
