Ngân hàng bài tập
SS
Cho hai hàm số $f(x)=mx^3+nx^2+px-\dfrac{5}{2}$ $(m,\,n,\,p\in\mathbb{R})$ và $g(x)=x^2+2x-1$ có đồ thị cắt nhau tại ba điểm có hoành độ lần lượt là $-3$, $-1$, $1$ (tham khảo hình vẽ).
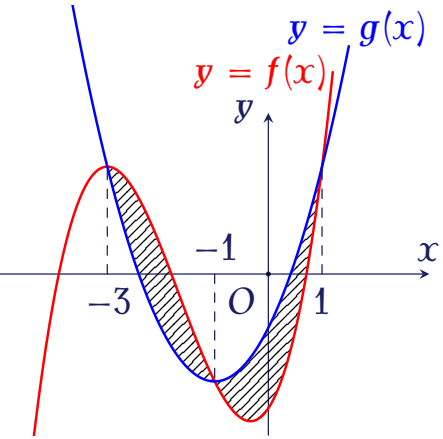
Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số $f(x)$ và $g(x)$ bằng
| $\dfrac{9}{2}$ | |
| $\dfrac{18}{5}$ | |
| $4$ | |
| $5$ |
1 lời giải
Chọn phương án C.
Theo đề bài ta có $f(x)$ và $g(x)$ cắt nhau tại các điểm có tọa độ là $(-3;2)$, $(-1;2)$ và $(1;2)$.
Lần lượt thay vào $f(x)$ ta được hệ phương trình $$\begin{cases}
-27m+9n-3p-\dfrac{5}{2}&=2\\
-m+n-p-\dfrac{5}{2}&=-2\\
m+n+p-\dfrac{5}{2}&=2
\end{cases}\Leftrightarrow\begin{cases}
m=\dfrac{1}{2}\\ n=\dfrac{5}{2}\\ p=\dfrac{3}{2}
\end{cases}$$
Vậy $f(x)=\dfrac{x^3}{2}+\dfrac{5x^2}{2}+\dfrac{3x}{2}-\dfrac{5}{2}$.
$\begin{aligned}
\blacksquare\,S_1&=\displaystyle\int\limits_{-3}^{-1}\left[f(x)-g(x)\right]\mathrm{\,d}x\\
&=\displaystyle\int\limits_{-3}^{-1}\left[\left(\dfrac{x^3}{2}+\dfrac{5x^2}{2}+\dfrac{3x}{2}-\dfrac{5}{2}\right)-\left(x^2+2x-1\right)\right]\mathrm{\,d}x\\
&=\displaystyle\int\limits_{-3}^{-1}\left[\dfrac{x^3}{2}+\dfrac{3x^2}{2}-\dfrac{x}{2}-\dfrac{3}{2}\right]\mathrm{\,d}x\\
&=2.
\end{aligned}$
\blacksquare\,S_1&=\displaystyle\int\limits_{-3}^{-1}\left[f(x)-g(x)\right]\mathrm{\,d}x\\
&=\displaystyle\int\limits_{-3}^{-1}\left[\left(\dfrac{x^3}{2}+\dfrac{5x^2}{2}+\dfrac{3x}{2}-\dfrac{5}{2}\right)-\left(x^2+2x-1\right)\right]\mathrm{\,d}x\\
&=\displaystyle\int\limits_{-3}^{-1}\left[\dfrac{x^3}{2}+\dfrac{3x^2}{2}-\dfrac{x}{2}-\dfrac{3}{2}\right]\mathrm{\,d}x\\
&=2.
\end{aligned}$
$\begin{aligned}
\blacksquare\,S_2&=\displaystyle\int\limits_{-1}^{1}\left[g(x)-f(x)\right]\mathrm{\,d}x\\
&=\displaystyle\int\limits_{-1}^{1}\left[\left(x^2+2x-1\right)-\left(\dfrac{x^3}{2}+\dfrac{5x^2}{2}+\dfrac{3x}{2}-\dfrac{5}{2}\right)\right]\mathrm{\,d}x\\
&=\displaystyle\int\limits_{-1}^{1}\left[-\dfrac{x^3}{2}-\dfrac{3x^2}{2}+\dfrac{x}{2}+\dfrac{3}{2}\right]\mathrm{\,d}x\\
&=2.
\end{aligned}$
\blacksquare\,S_2&=\displaystyle\int\limits_{-1}^{1}\left[g(x)-f(x)\right]\mathrm{\,d}x\\
&=\displaystyle\int\limits_{-1}^{1}\left[\left(x^2+2x-1\right)-\left(\dfrac{x^3}{2}+\dfrac{5x^2}{2}+\dfrac{3x}{2}-\dfrac{5}{2}\right)\right]\mathrm{\,d}x\\
&=\displaystyle\int\limits_{-1}^{1}\left[-\dfrac{x^3}{2}-\dfrac{3x^2}{2}+\dfrac{x}{2}+\dfrac{3}{2}\right]\mathrm{\,d}x\\
&=2.
\end{aligned}$
Vậy diện tích hình phẳng đã cho là $S=S_1+S_2=2+2=4$.
