Ngân hàng bài tập
SSS
Xét số phức $z$ thỏa mãn $|z+3-2i|+|z-3+i|=3\sqrt{5}$. Gọi $M,\,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức $P=|z+2|+|z-1-3i|$. Khi đó
| $M=\sqrt{26}+2\sqrt{5}$, $m=3\sqrt{2}$ | |
| $M=\sqrt{17}+\sqrt{5}$, $m=\sqrt{2}$ | |
| $M=\sqrt{26}+2\sqrt{5}$, $m=\sqrt{2}$ | |
| $M=\sqrt{17}+\sqrt{5}$, $m=3\sqrt{2}$ |
1 lời giải
Chọn phương án A.
Giả sử $S(x;y)$, $A(-3;2)$, $B(3;-1)$. Khi đó:
- $|z+3-2i|+|z-3+i|=|z-(-3+2i)|+|z-(3-i)|=SA+SB$
- $\overrightarrow{AB}=(6;-3)\Rightarrow AB=3\sqrt{5}$
Suy ra điểm $S$ nằm trên đoạn $AB$, tức là $x\in[-3;3]$.
Đường thẳng $AB$ có vectơ chỉ phương $\overrightarrow{AB}=(6;-3)$ nên nhận $\overrightarrow{n}=(1;2)$ làm vectơ pháp tuyến. Ta có phương trình $(x-3)+2(y+1)=0$ hay $x+2y-1=0$.
Vì $S\in AB$ nên $y=\dfrac{1-x}{2}$.
Khi đó $\begin{aligned}[t]
P&=|(x+2)+yi|+|(x-1)+(y-3)i|\\
&=\sqrt{(x+2)^2+y^2}+\sqrt{(x-1)^2+(y-3)^2}\\
&=\sqrt{(x+2)^2+\left(\dfrac{1-x}{2}\right)^2}+\sqrt{(x-1)^2+\left(\dfrac{-5-x}{2}\right)^2}\\
&=\dfrac{1}{2}\sqrt{5x^2+14x+17}+\dfrac{1}{2}\sqrt{5x^2+2x+29}.
\end{aligned}$
Xét $f(x)=\dfrac{1}{2}\sqrt{5x^2+14x+17}+\dfrac{1}{2}\sqrt{5x^2+2x+29}$ trên $[-3;3]$.
Ta có $f'(x)=\dfrac{5x+7}{2\sqrt{5x^2+14x+17}}+\dfrac{5x+1}{2\sqrt{5x^2+2x+29}}$.
Cho $f'(x)=0\Leftrightarrow x=-1$.
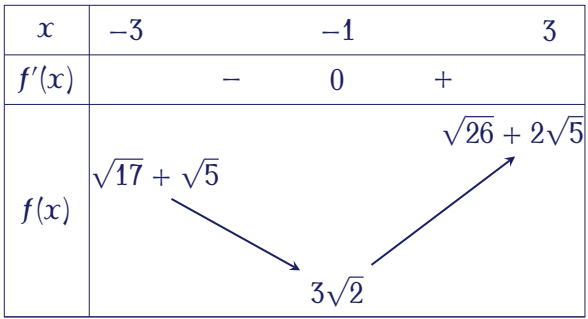
Vậy $M=\sqrt{26}+2\sqrt{5}$ và $m=3\sqrt{2}$.
