Có bao nhiêu giá trị nguyên của tham số a thuộc đoạn $[-10;10]$ để hàm số $$y=\big|-x^3+3(a+1)x^2-3a(a+2)x+a^2(a+3)\big|$$đồng biến trên khoảng $(0;1)$
| $21$ | |
| $10$ | |
| $8$ | |
| $2$ |
Chọn phương án B.
Đặt $\begin{aligned}[t]
f(x)&=-x^3+3(a+1)x^2-3a(a+2)x+a^2(a+3)\\
&=(x-a)^2(a+3-x).
\end{aligned}$
Ta có $f(x)=0\Leftrightarrow\left[\begin{aligned}&x=a\\ &x=a+3.\end{aligned}\right.$
Cho $\begin{aligned}[t]
f'(x)=0&\Leftrightarrow-3x^2+6(a+1)x-3a(a+2)=0\\ &\Leftrightarrow\left[\begin{aligned}&x=a\\ &x=a+2\end{aligned}\right.
\end{aligned}$
Khi đó $y=|f(x)|=\sqrt{f^2(x)}\Rightarrow y'=\dfrac{f(x)\cdot f'(x)}{\big|f(x)\big|}$.
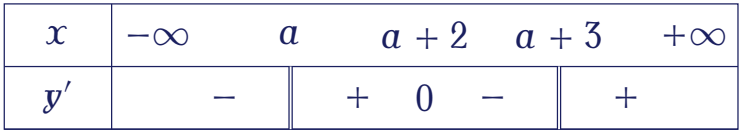
Dựa vào bảng xét dấu ta thấy yêu cầu bài toán thỏa mãn khi $$\left[\begin{aligned}
&\begin{cases}a\le0\\ a+2\ge1\end{cases}\\
&a+3\le3
\end{aligned}\right.\Leftrightarrow \left[\begin{aligned}
&-1\le a\le0\\
&a\le-3.
\end{aligned}\right.$$
Vậy có $10$ số nguyên $a$ thỏa mãn yêu cầu bài toán.
