Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB=1$, $BC=2$, $AA'=2$ (tham khảo hình bên).
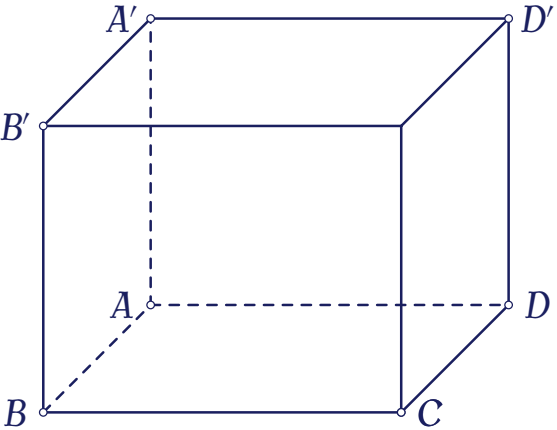
Khoảng cách giữa hai đường thẳng $AD'$ và $DC'$ bằng
| $\sqrt{2}$ | |
| $\dfrac{\sqrt{6}}{2}$ | |
| $\dfrac{2\sqrt{5}}{5}$ | |
| $\dfrac{\sqrt{6}}{3}$ |
Chọn phương án D.
Đặt hình hộp chữ nhật đã cho vào hệ trục tọa độ $Oxyz$ sao cho $A\equiv O(0;0;0)$, điểm $B\in Ox$, $D\in Oy$, $A'\in Oz$.
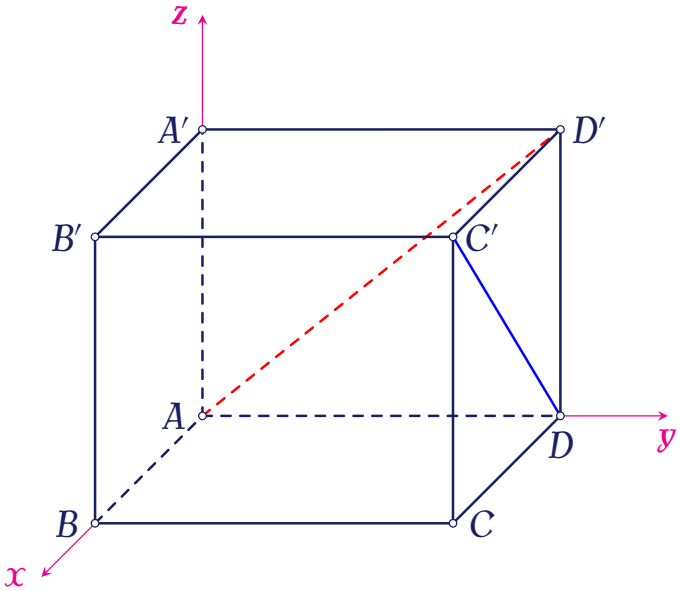
Ta có $A(0;0;0)$, $D(0;2;0)$, $D'(0;2;2)$, $C'(1;2;2)$. Khi đó $\overrightarrow{AD'}=(0;2;2)$, $\overrightarrow{DC'}=(1;0;2)$, $\overrightarrow{AD}=(0;2;0)$.
Khi đó $\left[\overrightarrow{AD'},\overrightarrow{DC'}\right]=(4;2;-2)$.
- Đường thẳng $AD'$ đi qua điểm $A$ và có vectơ chỉ phương $\overrightarrow{AD'}$.
- Đường thẳng $DC'$ đi qua điểm $D$ và có vectơ chỉ phương $\overrightarrow{DC'}$.
Vậy $\begin{aligned}[t]
\mathrm{d}\big(AD',DC'\big)&=\dfrac{\bigg|\left[\overrightarrow{AD'},\overrightarrow{DC'}\right]\cdot\overrightarrow{AD}\bigg|}{\bigg|\left[\overrightarrow{AD'},\overrightarrow{DC'}\right]\bigg|}\\
&=\dfrac{|4\cdot0+2\cdot2-2\cdot0|}{\sqrt{4^2+2^2+(-2)^2}}=\dfrac{\sqrt{6}}{3}.
\end{aligned}$
Chọn phương án D.
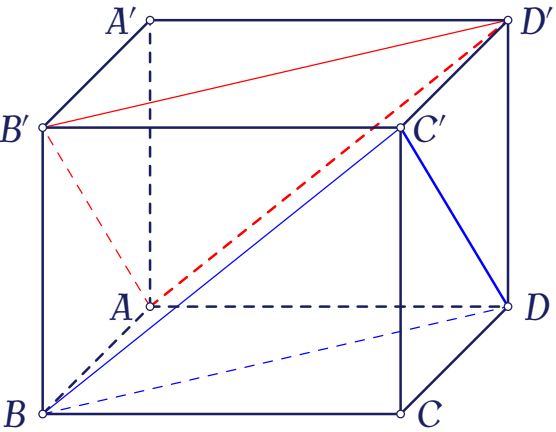
Ta có $AD'\subset(AD'B')$, $DC'\subset(DC'B)$. Vì $(AD'B')\parallel(DC'B)$ nên $\mathrm{d}\big(AD',DC'\big)=\mathrm{d}\big((AD'B'),(DC'B)\big)=\mathrm{d}\big(A,(DC'B)\big)$.
Vì $AC$ cắt $BD$ tại trung điểm mỗi đường nên $\mathrm{d}\big(A,(DC'B)\big)=\mathrm{d}\big(C,(DC'B)\big)$.
Gọi $CH$ là đường cao $\triangle BCD$, gọi $CK$ là đường cao $\triangle CC'H$.
Vì $\begin{cases}
BD\perp CH\\ BD\perp CC'
\end{cases}$ nên $BD\perp CK$.
Lại vì $CK\perp C'H$ nên $CK\perp(BDC')$. Do đó $\mathrm{d}\big(C,(DC'B)\big)=CK$.
Ta có $\begin{aligned}[t]
\dfrac{1}{CK^2}&=\dfrac{1}{CH^2}+\dfrac{1}{CC'^2}\\
&=\left(\dfrac{1}{CB^2}+\dfrac{1}{CD^2}\right)+\dfrac{1}{CC'^2}\\
&=\left(\dfrac{1}{2^2}+\dfrac{1}{1^2}\right)+\dfrac{1}{2'^2}=\dfrac{3}{2}.
\end{aligned}$
Suy ra $CK^2=\dfrac{2}{3}$. Vậy $CK=\sqrt{\dfrac{2}{3}}=\dfrac{\sqrt{6}}{3}$.
