Ngân hàng bài tập
A
Cho hình chóp đều $S.ABCD$ có đáy bằng a và chiều cao bằng $\dfrac{\sqrt{3}a}{6}$. Góc giữa mặt phẳng $(SCD)$ và mặt phẳng đáy bằng
| $45^\circ$ | |
| $90^\circ$ | |
| $60^\circ$ | |
| $30^\circ$ |
1 lời giải
Chọn phương án D.
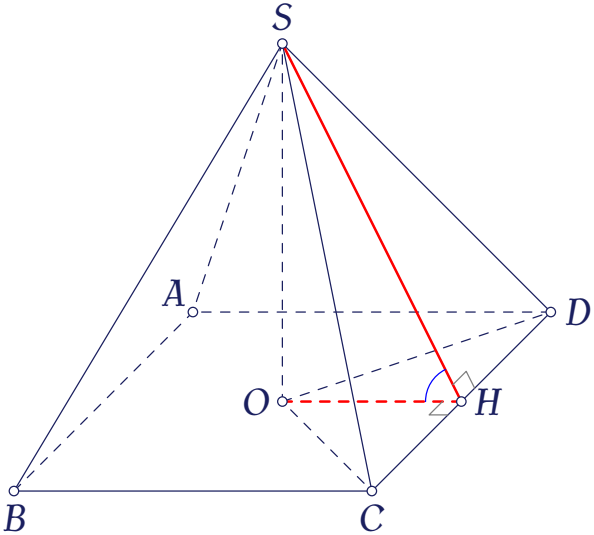
Gọi $O$ là tâm mặt đáy, $H$ là trung điểm cạnh $CD$.
Vì $SH\perp CD$ và $OH\perp CD$ nên $\big((SCD),(ABCD)\big)=\big(SH,OH\big)=\widehat{SHO}$.
Xét tam giác $SOH$ vuông tại $O$ ta có $SO=h=\dfrac{\sqrt{3}a}{6}$ và $OH=\dfrac{AD}{2}=\dfrac{a}{2}$.
Khi đó $\tan\widehat{SHO}=\dfrac{SO}{OH}=\dfrac{\dfrac{\sqrt{3}a}{6}}{\dfrac{a}{2}}=\dfrac{\sqrt{3}}{3}$.
Suy ra $\widehat{SHO}=30^\circ$.
