Ngân hàng bài tập
SS
Cho hàm số $y=f(x)$ xác thực trên tập số thực $\mathbb{R}$ và có đồ thị $f'(x)$ như hình vẽ.
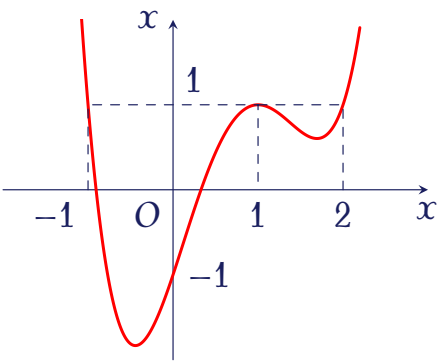
Đặt $g(x)=f(x)-x$, hàm số $g(x)$ nghịch biến trên khoảng
| $(1;+\infty)$ | |
| $(-1;2)$ | |
| $(2;+\infty)$ | |
| $(-\infty;-1)$ |
1 lời giải
Chọn phương án B.
Ta có $g'(x)=f'(x)-1$.
Hàm số $g(x)$ nghịch biến khi $$\begin{aligned}
g'(x)\leq0&\Leftrightarrow f'(x)-1\leq0\\
&\Leftrightarrow f'(x)\leq1\\
&\Leftrightarrow x\in[-1;2]
\end{aligned}$$
Vậy $g(x)$ nghịch biến trên khoảng $(-1;2)$.
